Adição, subtração, multiplicação e divisão de frações
Veja como resolcver questões do Enem sobre números decimais e frações. Também vale para transformar “números com vírgula” em frações, ou vice-versa. A mágica acontece quando você aprende. É simples. vem, porque sempre cai.
Você sabia que os números mais utilizados em nosso dia a dia podem ser representados por frações? Sim, isso mesmo. Além disso, quando falamos em porcentagem, escalas, análise de dados entre outros números, também podemos escrevê-los sob forma de fração.
O conceito de fração deve ser bem compreendido para que possamos compreender dados que nos são apresentados a todo momento.
Estes dados são representados por números inteiros, fracionários, infográficos, mapas ou tabelas e ajudam a ilustrar dados estatísticos de economia, política, ciências, saúde, entre tantas informações que lidamos todos os dias.
Introdução às frações – Veja agora com o professor Lucas Borghesan, do canal do Cuso Enem Gratuito no Youtube, o que são frações e como simplificá-las.
O que é uma Fração?
Uma fração é “uma parte” de um todo. Os cantores e compositores Philippe Seabra e André X, escreveram uma canção para a banda Plebe Rude, que fala de fração.
Veja agora uma estrofe da letra de “Até quando Esperar”, e veja o vídeo completo no final do post:
Com tanta riqueza por aí
Onde é que está? Cadê sua fração?
Com tanta riqueza por aí
Onde é que está? Cadê sua fração?
A fração, portanto, ou número fracionário é uma forma diferente de representar um quociente. Dizemos que uma fração é uma pequena porção de um todo e é representada por:![]()
Veja a imagem abaixo que representa um bolo (que é o inteiro). Esse bolo foi repartido em 8 fatias iguais. 5 dessas fatias foram comidas e então sobraram 3.
Qual a fração que representa o que sobrou do bolo? Resposta: Então, cinco oitavos do bolo foram consumidos.
Resposta: Então, cinco oitavos do bolo foram consumidos.
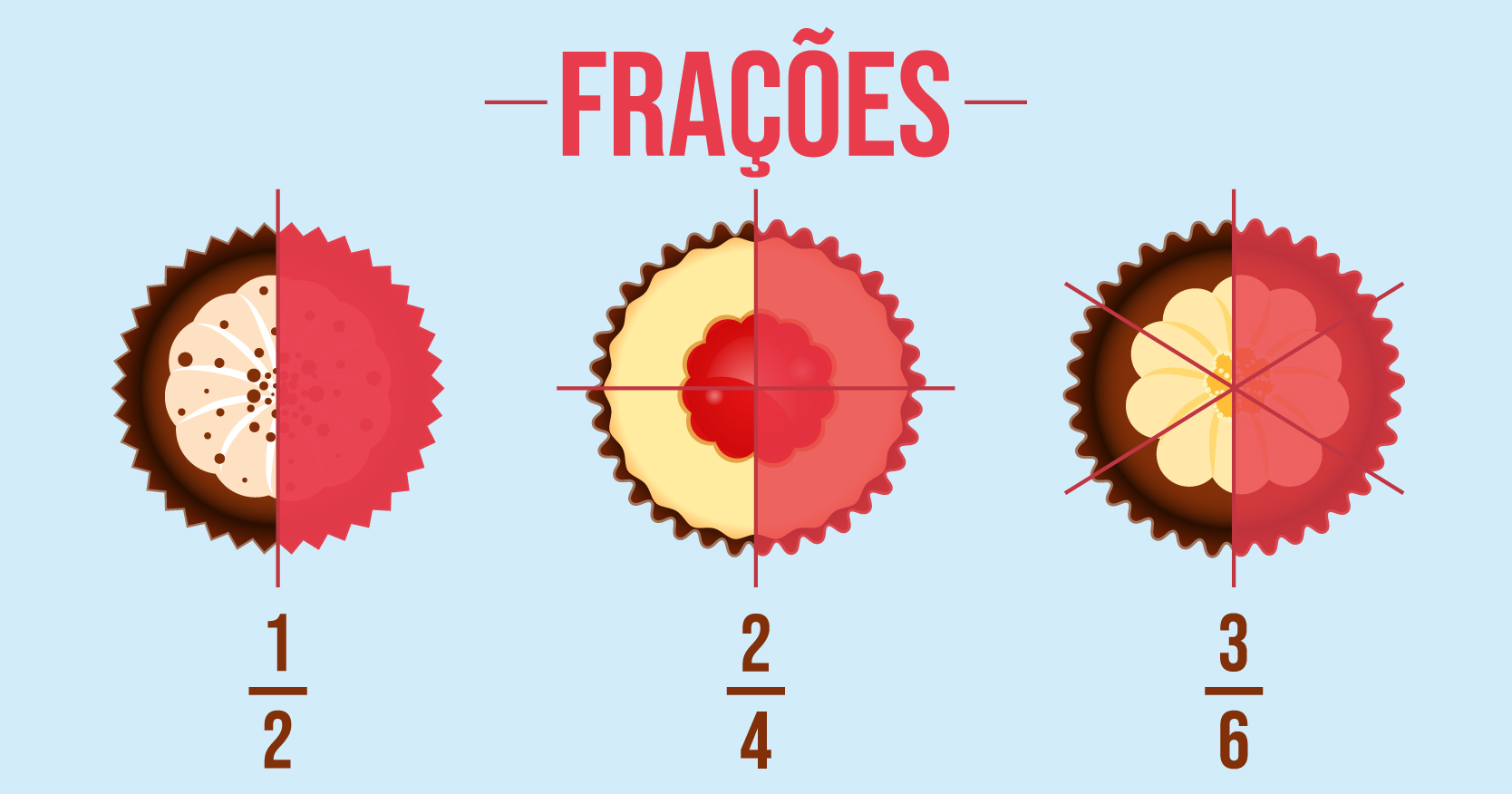
Agora que você já entendeu o conceito de fração, vamos falar das frações equivalentes. Elas são importantes para a resolução de problemas que envolvem simplificação.
As Frações equivalentes
Veja a imagem abaixo:

Observe que as três imagens são idênticas em tamanho forma e cor. O que difere uma da outra é o número de divisões que elas têm.
Se compararmos as três frações ou simplificarmos teremos o mesmo valor, então dizemos que essas frações são equivalentes.
![]()
Podemos concluir que:
“Quando multiplicamos ou dividimos o numerador e o denominador de uma fração por um mesmo número, diferente de zero, essa não se altera e as frações assim obtidas são chamadas de equivalentes.”

Veja as operações básicas:
Adição e subtração
Temos dois casos que envolvem essas operações:
Frações com o mesmo denominador
Nesse caso adicionamos ou subtraímos os numeradores e conservamos os denominadores. Isso é importante:
Nunca se soma ou subtrai denominador de uma fração.
Veja o exemplo:
![]()
Frações com denominadores diferentes
Nesse caso devemos realizar o MMC entre os denominadores.
A regra é dividir o denominador pelo MMC e multiplicar pelo numerador em cada fração.
Veja o exemplo:
![]()
Multiplicação entre frações:
Multiplicamos numeradores com numeradores e denominadores com denominadores. Observe:
![]()
Neste caso ainda podemos simplificar o resultado, isto é, achar seu equivalente:
(24 ÷12)/(60÷12)=2/5
Divisão entre frações:
A divisão de frações deve ser transformada em uma multiplicação: conservamos a primeira fração e invertemos a segunda.
Veja o exemplo:
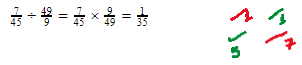
Nesse caso, simplificamos as frações antes de continuar a multiplicação. Treine que fica muito fácil!
Potências e Raízes:
As potências e raízes são inversas e, por isso veremos as duas num mesmo tópico.
Para elevarmos uma fração a um expoente, elevamos o numerador e também o denominador.
Aqui vai um exemplo:
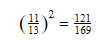
Para extrair uma raiz de uma fração, extraímos tanto do numerador como o denominador. Veja abaixo:
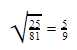
Veja agora como resolver questões com a Divisão de números decimais, com casas depois da vírgula.
Artimética: Como fazer a Divisão com vírgulas
Acompanhe com o professor Lucas Borguezan, do canal do Curso Enem Gratuito
Exercícios sobre Frações
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(UNCISAL/2018)
De acordo com a Organização Mundial das Nações Unidas, cada pessoa necessita de 3,3 m3/mês de água para atender suas necessidades de consumo e higiene. Para saber qual é a quantidade de água que deve ser ingerida diariamente, é necessário avaliar a idade, o sexo, o hábito de vida e a saúde da pessoa. Sobre essa temática, considere as seguintes informações:
• Uma recomendação é ingerir 35 ml de água a cada quilograma de massa, diariamente.
• Em uma pessoa sadia, há equilíbrio entre a água ingerida e a eliminada. Essa eliminação ocorre sob a forma de urina (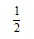 da água ingerida), nas fezes (
da água ingerida), nas fezes (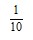 da água ingerida) e na transpiração (o restante da água ingerida).
da água ingerida) e na transpiração (o restante da água ingerida).
• Uma grande porcentagem do corpo de um ser humano adulto é formada por moléculas de água e isso representa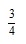 de seu peso em água.
de seu peso em água.Considerando o exposto, assinale a alternativa correta.
CorretoResposta correta!
-
Pergunta 2 de 10
2. Pergunta
(UNIMONTES MG/2008)
Ao escrevermos frações menores do que 1, cujos numeradores e denominadores são números inteiros positivos de um algarismo, escrevemos
CorretoResposta correta!
-
Pergunta 3 de 10
3. Pergunta
(FGV /2007)
Considere as frações
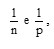 com n e p sendo números irracionais. Sobre o resultado da soma
com n e p sendo números irracionais. Sobre o resultado da soma 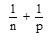 afirma-se que pode ser:
afirma-se que pode ser:I. inteiro não nulo;
II. racional não inteiro;
III. irracional;
IV. zero;
V. imaginário puro.É correto apenas o que está contido em
CorretoResposta correta!
-
Pergunta 4 de 10
4. Pergunta
(UFTM/2007)
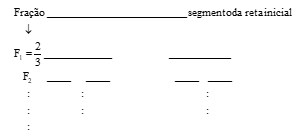
Toma-se um segmento de reta inicial de tamanho 1. Divide-se o segmento de reta em 3 partes iguais e tira-se a parte do meio. Cada uma das duas partes remanescentes também é dividida em 3 partes iguais e as respectivas partes do meio também são retiradas. Procede-se de maneira análoga indefinidamente, conforme figura, sendo que a fração do que sobrou do segmento de reta inicial na 1.ª divisão é denotado por F1, na 2.ª divisão, por F2 e na enésima divisão, por Fn.
Então, a soma de todas as frações, após n divisões é:
 Correto
CorretoResposta correta!
-
Pergunta 5 de 10
5. Pergunta
(ENEM/2001)
A distribuição média, por tipo de equipamento, do consumo de energia elétrica nas residências no Brasil é apresentada no gráfico.

Em associação com os dados do gráfico, considere as variáveis:
I. Potência do equipamento.
II. Horas de funcionamento.
III. Número de equipamentos.O valor das frações percentuais do consumo de energia depende de
CorretoResposta correta!
-
Pergunta 6 de 10
6. Pergunta
(FUVEST SP/1998)
A soma das frações irredutíveis, positivas, menores do que 10, de denominador 4, é:
CorretoResposta correta!
-
Pergunta 7 de 10
7. Pergunta
(Enem, 2017)
Uma escola organizou uma corrida de revezamento 4 x 400 metros, que consiste em uma prova esportiva na qual os atletas correm 400 metros cada um deles, segurando um bastão, repassando-o de um atleta para outro da mesma equipe, realizando três trocas ao longo do percurso, até o quarto atleta, que cruzará a linha de chegada com o bastão. A equipe ganhadora realizou a prova em um tempo total de 325 segundos. O segundo corredor da equipe ganhadora correu seus 400 metros 15 segundos mais rápido do que o primeiro; já o terceiro realizou seus 400 metros 5 segundos mais rápido que o segundo corredor, e o último realizou seu percurso em 3/4 do tempo realizado pelo primeiro.
Qual foi o tempo, em segundo, em que o último atleta da equipe ganhadora realizou seu percurso de 400 metros?
CorretoResposta correta!
-
Pergunta 8 de 10
8. Pergunta
(ESA-81)
Um clube de futebol tem 40 jogadores, dos quais apenas 11 são considerados titulares. A razão entre o número de titulares e o número de jogadores é:
CorretoResposta correta!
-
Pergunta 9 de 10
9. Pergunta
(Enem-2011)
O pantanal é um dos mais valiosos patrimônios naturais do Brasil. É a maior área úmida continental do planeta – com aproximadamente 210 mil km2, sendo 140 mil km2 em território brasileiro, cobrindo parte dos estados de Mato Grosso e Mato Grosso do Sul. As chuvas fortes são comuns nessa região. O equilíbrio desse ecossistema depende, basicamente, do fluxo de entrada e saída de enchentes. As cheias chegam a cobrir até 2/3 da área pantaneira. Durante o período chuvoso, a área alagada pelas enchentes pode chegar a um valor aproximado de:
CorretoResposta correta!
-
Pergunta 10 de 10
10. Pergunta
(UFSCar SP/2003)
Somando-se 4 ao numerador de certa fração, obtém–se outra igual a 1. Subtraindo-se 1 do denominador da fração original, obtém-se outra igual a 1/2. Os termos da fração original A/B representam os votos de dois candidatos, A e B, que foram para o 2º turno de uma eleição, onde o candidato B obteve
CorretoResposta correta!

Sobre o(a) autor(a):
Wania Maria de A. Pereira - A professora Wania Maria de A. Pereira é graduada em Física e Matemática pela Universidade Federal de Santa Maria (UFSM) e é Psicopedagoga com enfoque em Gestão de Pessoas (UNC) e especialista em Educação a Distância (SENAC- SC). Atuou na rede particular, estadual e municipal por 26 anos no Estado de Santa Catarina. Autora de diversos materiais didáticos para universidades públicas e privadas na área de Matemática, Metodologia de Ensino de Matemática e Psicopedagogia. Atualmente trabalha na área de Projetos de Tecnologias Digitais de Informação e Comunicação (TDICs). LinkedIn: https://www.linkedin.com/in/wmariaap/.
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.