Teoria dos conjuntos numéricos, agrupamentos e classificações
Você já notou que temos o hábito de separar as coisas por semelhança, cor, tamanho, tipo ou alguma coisa em comum? Classificar e separar faz parte de nosso desenvolvimento matemático mais básico e tem relação com a Teoria dos conjuntos. Vem revisar a Teoria dos conjuntos com a gente no Curso Enem Gratuito!
A Teoria dos Conjuntos estuda como selecionar, agrupar e classificar elementos. Nesta aula, você compreenderá os conceitos de conjuntos e subconjuntos. Além disso, verá seus elementos e suas representações através de chaves e diagrama de Venn. Por fim, conseguirá resolver problemas que envolvem relações de pertinência ou relações de inclusão.
A teoria dos conjuntos no dia a dia
Primeiramente, vamos observar como a teoria dos conjuntos numéricos está presente em nossas rotinas. Em nossa rotina, temos a tendência de selecionar coisas para depois organizar.
Em geral, agrupamos nossos pertences por uma característica que eles têm em comum. Além disso, classificamos ou damos nome a esses grupos.
Um exemplo: algumas pessoas organizam seus materiais escolares agrupando canetas, lápis, lapiseiras em um estojo. Esse estojo pode ser um conjunto de materiais de escrever. Figura 1 – Separamos lápis e canetas em um estojo. A foto mostra estojo com lápis de cor e outro com canetas coloridas. Veja como fazer ótimos resumos de mão no nosso vídeo!
Figura 1 – Separamos lápis e canetas em um estojo. A foto mostra estojo com lápis de cor e outro com canetas coloridas. Veja como fazer ótimos resumos de mão no nosso vídeo!
Do mesmo modo, colocamos diversos cadernos em uma pilha e livros em outra. Assim, organizamos nossos materiais em diversos conjuntos.
Com isso podemos afirmar que:
Um conjunto é um agrupamento de elementos.
Introdução à Teoria dos Conjuntos
Veja agora com o professor Lucas Borguezan um resumo de introdução que vai ajudar você no domínio desta matéria.
As dicas do professor Lucas:
- Em nossa rotina, temos a tendência de selecionar coisas para depois organizar. Em geral, agrupamos nossos pertences por uma característica que eles têm em comum.
- Além disso, classificamos ou damos nome a esses grupos.
- Do mesmo modo, colocamos diversos cadernos em uma pilha e livros em outra. Assim, organizamos nossos materiais em diversos conjuntos.
- Com isso, podemos afirmar que um conjunto é um agrupamento de elementos.
- Os conjuntos normalmente são representados por letras maiúsculas e os elementos são delimitados por chaves ou diagrama de Venn.
- Nesta aula acima, o professor Lucas te ensina a linguagem matemática dos conjuntos numéricos e te mostra como ocorrem as relações de pertinência.
A simbologia do que pertence, ou não pertence
Os conjuntos normalmente são representados por letras maiúsculas e os elementos são delimitados por chaves ou diagrama de Venn.
Em primeiro lugar, vamos ver alguns exemplos de conjuntos representados através de chaves:
Cores primárias: C = {amarelo, azul, vermelho}
Dinheiro brasileiro: D = {centavos, real}
Flores: F = {rosa, violeta, sempre-viva, amarílis, cravo, …}
Sob o mesmo ponto de vista, vamos ver agora exemplos de representação de conjuntos com diagrama de Venn. Esse diagrama é facilita a visualização da teoria dos conjuntos:
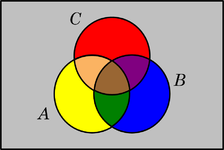
O diagrama de Venn é uma linha fechada que pode ter qualquer forma. Ele serve para delimitar os elementos.
Conjuntos especiais:
Bem como a representação através de chaves e o diagrama de Venn, você precisa entender dois tipos de conjuntos especiais:
a) Conjunto vazio: é um conjunto sem elementos e é representado por { } ou ∅.
b) Conjunto unitário: é um conjunto que tem um único elemento. Ex: A = {10}.
Além disso, é importante que você saiba que existe uma relação entre conjuntos e elementos que denominamos Relação de Pertinência.
Relação de Pertinência
Antes de mais nada, vamos definir o que é relação de pertinência. Essa relação analisa se um elemento pertence ou não a um conjunto.
Quer um exemplo? Vamos construir um conjunto de números naturais ímpares menores que 20:
Sabemos que os números naturais são aqueles que usamos para a contagem:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 …
Esse é um conjunto infinito.
Tirando os números ímpares menores que 20, temos um novo conjunto que vamos chamar de I:
I = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
Até agora, selecionamos, agrupamos e classificamos. Se alguém perguntar a você se o número 10 pertence ao conjunto I, o que você responderia?
- Não, 10 não pertence ao conjunto I. Isso porque o número 10 não é um número ímpar, logo ele não está dentro do conjunto I.
- E o número 13 pertence ao conjunto I? Sim, porque ele é um número ímpar menor que 20.
- Em suma, essa é a análise da Relação de Pertinência que faz a relação entre elementos e um conjunto.
Os Conjuntos Numéricos
Acompanhe com o professor Lucas a introdução aos Conjuntos Numéricos.
As dicas do Lucas sobre os Conjuntos Numéricos:
- Sabe aqueles grupinhos característicos que tem em todo ensino médio? Vamos pensar juntos: toda escola tem aquele grupo que é mais bagunceiro; tem a galera do fundão; tem o pessoal mais dedicado e estudioso; a galera mais ligada em rede socia;, os que tocam algum instrumento… Enfim, são muitos os grupinhos.
- Mas, sabe o que todos esses grupos tem em comum? Os membros de cada grupo têm características parecidas, por isso se identificam!
- Em cada agrupamento eles formam conjuntos e na matemática nós chamamos de conjuntos numéricos!
- Vem que o professor Lucas te explica 🙂
Linguagem matemática dos conjuntos numéricos
Assim como a compreensão da simbologia dos conjuntos, é necessário que você saiba sua linguagem matemática. Como podemos escrever a frase 10 não pertence ao conjunto I na linguagem matemática? Podemos escrever essa expressão: 10 ∉ I.
O símbolo ∉ indica não pertence.
Sob o mesmo ponto de vista, como podemos escrever, na linguagem matemática, a frase 13 pertence ao conjunto I? Escrevemos assim: 13 ∈ I.
O símbolo ∈ significa pertence.
O que são subconjuntos?
Vamos falar da Relação de Inclusão propriamente dita? Anteriormente, temos que mostrar o que é um subconjunto.
Em primeiro lugar, para entender o que são subconjuntos, observe o exemplo anterior (aquele que vimos no item Relação de Pertinência). Vamos definir que o conjunto dos números naturais é o conjunto a ser analisado. Dessa forma, o conjunto dos números pares e o conjunto dos números ímpares são subconjuntos do conjunto dos números naturais.
Logo, subconjuntos são pequenos conjuntos formados com os elementos do conjunto maior que denominamos Universo.
De acordo com o que vimos acima, vamos representar esses conjuntos em linguagem matemática:
a) Conjunto dos números naturais: N = {0,1,2,3,4,5,6,7,8,9…}
b) Conjunto dos números pares: P = { 0, 2, 4, 6 …}
c) Conjunto dos números ímpares: U = {1, 3, 5, 7, 9…}
d) Conjunto dos números ímpares menores que 20:
I = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
Os conjuntos dos itens b) c) d) são subconjuntos do conjunto dos números naturais. E são apenas alguns exemplos dos infinitos subconjuntos que se originam do conjunto maior.
Relação de Inclusão – teoria dos conjuntos
A Relação de Inclusão analisa se subconjuntos estão dentro de outros conjuntos maiores.
Primeiramente, vamos aprender quais são os símbolos usados nas relações de inclusão são:
a) Contido: ⊂
b) Não está contido: ⊄
c) Contém: ⊃
d) Não contém: ⊅
Agora, vamos resolver dois tipos de problemas sobre teoria dos conjuntos que apareceram em provas de vestibulares:
1. (F. C. Chagas) Se A = {∅, 3, {3}, {2, 3}}, então:
a) {2, 3} ⊂ A
b) 2 ∈ A
c) ∅ ∉ A
d) 3 ⊂ A
e) {3} ∈ A
Antes de mais nada, para resolver esse tipo de questão, temos que analisar todos os dados do problema.
O primeiro dado muito importante é o conjunto dado no enunciado:
A = {∅, 3, {3}, {2, 3}}
Note que temos elementos desse conjunto que são conjuntos menores. Dizemos que {3} e {2, 3} são elementos de A, logo só podemos usar a relação de pertinência entre eles e o conjunto A.
O símbolo ∅ indica o conjunto vazio.
a) {2, 3} ⊂ A é falsa, porque {2, 3} é elemento de A e não é subconjunto de A. O sinal ⊂ indica uma relação de inclusão que é usada entre conjunto e subconjunto.
b) 2 ∈ A é falsa, porque não tem elemento 2 no conjunto A.
c) ∅ ∉ A é falsa, porque o elemento vazio pertence ao conjunto A.
d) 3 ⊂ A é falsa, porque não usamos sinal de inclusão entre elemento e conjunto. O correto é 3 ∈ A.
e) {3} ∈ A está correta, pois {3} é elemento do conjunto A.
Fazer esse tipo de análise para resolver esse tipo de problema pode te ajudar muito. Lembre-se de fazer isso para resolver questões que envolvem conjuntos, elementos, subconjuntos. Essa análise também é útil para resolver questões que envolvem símbolos das relações de Pertinência e as relações de Inclusão.
Para reforçar essa ideia de Relações acesse nossa aula escrita sobre esse assunto.
Quer outro exemplo?
2. (UFGO) Nas sentenças abaixo, assinalam-se com V as sentenças verdadeiras e com F as falsas:
{2} ∈ {0, 1, 2}
∅ ⊂ {5, 6, 7}
∅ ∈ {∅, 4}
5 ∈ {3, {5, 1}, 4}
{5, 6} ⊃ {5, 6, 7}
Nesta ordem, a alternativa CORRETA é:
a) F, V, V, F, F
b) V, F, F, V, F
c) F, V, V, F, V
d) V, F, F, V, V
A resolução desse tipo de problema é mais elaborada. Temos que analisar cada afirmação uma a uma:
- {2} ∈ {0, 1, 2}
Para essa afirmação, temos que analisar se {2} está dentro do conjunto {0, 1, 2}. Com isso, percebemos que o elemento 2 está no conjunto, mas {2} não está, então é F.
- ∅ ⊂ {5, 6, 7}
O conjunto vazio é subconjunto de qualquer conjunto, logo está contido no conjunto {5, 6, 7}. A afirmação é V.
- 3. ∅ ∈ {∅, 4}
O conjunto vazio aparece como elemento desse conjunto, então podemos usar o símbolo de pertence. A afirmação é V.
- 5 ∈ {3, {5, 1}, 4}
Essa afirmação é falsa porque não tem elemento 5 no conjunto. O que temos como elemento do conjunto é {5, 1}. A afirmação é F.
- {5, 6} ⊃ {5, 6, 7}
O símbolo contém é usado quando o primeiro conjunto tem um número de elementos maior que o segundo. Além disso, o segundo conjunto deve ter elementos no primeiro conjunto. Logo, a afirmação é F.
A alternativa correta é a alternativa a.
Vídeo sobre teoria dos conjuntos
Para finalizar, assista ao vídeo abaixo, em que o professor Lucas Borguezan, do canal do Curso Enem Gratuito, explica sobre esse assunto!
Em conclusão, nesta aula você aprendeu que a teoria dos conjuntos vem do modo como selecionamos, classificamos, agrupamos as coisas (objetos, pessoas, etc). Além disso, você compreendeu que conjunto é um agrupamento de elementos e como podemos representar esses conjuntos. Por fim, apresentamos o conjunto vazio, unitário, as relações de pertinência e as relações de inclusão.
Exercícios
1. Sendo A = {1, 2, {1}, {2, 3}}, qual das proposições abaixo é FALSA?
a) 1 ∈
b) {3} ∈
c) {1} ∈
d) A possui quatro elementos.
e) {1, 2, 3} ∈
2. Dado o conjunto A = {1, {2}, 2}, qual das relações abaixo é FALSA?
a) {2} ∈ A
b) {1} ∈ A
c) {1, 2} ⊂ A
d) {2} ⊂ A
e) {2, {2}} ⊂ A
3. (Mack – SP) Dado o conjunto A = {3, {3}} e as proposições:
I. 3 ∈ A
II. {3} ⊂ A
III. {3} ∈ A
Então:
a) apenas as proposições I e II são verdadeiras
b) apenas as proposições II e III são verdadeiras
c) apenas as proposições I e III são verdadeiras
d) todas as proposições são verdadeiras
e) nenhuma proposição é verdadeira
Gabarito: 1.B 2.B 3.D





