Triângulo retângulo: características e Teorema de Pitágoras
Os triângulos retângulos são os objetos centrais no estudo da trigonometria e suas aplicações são infinitas em áreas como a Física, a Engenharia e o Design. Veja no resumo os macetes para você gabaritar os triângulos na matemática do Enem.
Entender as características e propriedades do triângulo retângulo com certeza ajuda a resolver muitas questões de Matemática no Enem e nos vestibulares. Aprenda tudo sobre essa figura geométrica nesta aula!
O que é um triângulo retângulo
Os triângulos retângulos são polígonos de três lados e três vértices onde encontramos dois ângulos agudos e um ângulo reto (formando um ângulo de 90º). O ângulo reto é a característica principal desse triângulo e é assim que o diferenciamos de outros triângulos.
Características do triângulo retângulo
O ângulo reto é a característica principal do triângulo retângulo e é assim que o diferenciamos de outros tipos de triângulos. Além do ângulo reto, outra característica interessante do triângulo retângulo é que seus lados têm nomes específicos que os outros triângulos não têm.
Lados do triângulo retângulo
O triângulo retângulo é formado por dois catetos e uma hipotenusa. Conheça melhor os lados do triângulo retângulo a seguir.
Hipotenusa
A hipotenusa é o lado com a medida maior e se localiza do lado oposto ao vértice onde está o ângulo reto. No triângulo da figura abaixo a hipotenusa é representada pelo lado a.
Catetos
Catetos são os lados que ajudam a formar o ângulo reto do triângulo. No triângulo da figura abaixo, são representados por c e b.
Estudo e aplicações
Por ser um tipo especial de triângulo, a literatura especializada dedica capítulos inteiros a seu estudo, pois essa figura é o pilar dos estudos da trigonometria.
Veja no resumo do professor de matemática Sérgio Sarkis, do canal do Curso Enem Gratuito, uma introdução ao Triângulo Retângulo:
Na história, os povos antigos, já utilizavam o triângulo retângulo como referência para a construção de suas casas e cidades, para projetar suas lavouras e até controlar o tempo.
Os egípcios, por exemplo, já tinham o conhecimento de triângulos de lados 3, 4, 5 unidades e os utilizavam como instrumento de medida na engenharia. Seu ângulo reto dava o equilíbrio que precisavam nos projetos.
Hoje, usamos sua teoria para projetos de construção civil, naval, agrimensura, topografia e também para cálculos de astronomia, como a distância de dois planetas. Suas aplicações são infinitas e por isso é que devemos conhecer sua teoria a fundo!
Teorema de Pitágoras
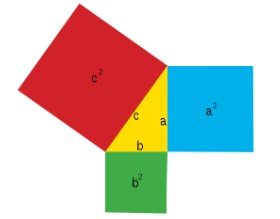
O Teorema de Pitágoras enuncia que, em um triângulo retângulo, a soma dos quadrados dos catetos é igual ao quadrado a hipotenusa. Ou seja, “se um triângulo retângulo tem catetos de medidas b e c e a hipotenusa de medida a, então: a² = b² + c².”
O Teorema de Pitágoras tem esse nome porque o triângulo retângulo da demonstração de Euclides recebeu o nome de Pitagórico e, assim, o Teorema sobre essa demonstração surgiu como o Teorema de Pitágoras:
Resumo sobre o Teorema de Pitágoras
Veja agora com o professor Lucas Borguezan uma introdução bem simples e rápida para você dominar o Teorema de Pitágoras. Aprenda a resolver as questões:
Exemplo do uso do Teorema de Pitágoras
Uma escada medindo 4 metros tem uma de suas extremidades apoiada no topo de um muro, e a outra extremidade dista 2,4 m da base do muro. A altura desse muro é:
A) 2,3m B) 3,0m C) 3,2m D) 3,8m E) 1,6m
Resolução:
Nesta situação, podemos aplicar o teorema de Pitágoras.
Onde:
h = b = ?
c = 2,4m
a = 4m
Substituindo no Teorema de Pitágoras, temos:
a² = b² + c²
h2 + (2,4)2 = 42
h2 + 5,76 = 16
Isolamos h²:
h2 = 16 – 5,76
Subtraímos:
h2 = 10,24
E extraímos a raiz quadrada (que é a operação inversa da potenciação) de
10,24:
h = 3,2 m.
Logo, a altura do muro é de 3,2 m.
Relações métricas dos triângulos retângulos
Ao estudar os triângulos retângulos não podemos deixar de estudar suas relações métricas. Relações métricas são operações que envolvem as medidas dos lados e altura de um triângulo, quando este tem seu ângulo de 90º partido ao meio por uma bissetriz, gerando dois triângulos menores.
Veja as relações métricas com exercícios resolvidos agora, com o professor Lucas Borguezan:
Essas relações são obtidas através da teoria da semelhança entre triângulos. Observe a figura abaixo:
Perceba que temos dois triângulos, onde o primeiro tem seus lados iguais a c, m e h. O outro triângulo tem seus lados iguais a b, n e h.
Dizemos que:
- m é a projeção do cateto c sobre a hipotenusa a do triângulo.
- n é a projeção do cateto b sobre a hipotenusa a do triângulo.
- h é a altura do triângulo.
- c e b são os catetos do triângulo.
As relações métricas em um triângulo retângulo são:
- “O quadrado da medida da altura relativa à hipotenusa é igual ao produto das medidas das projeções ortogonais dos catetos sobre a hipotenusa.”
- “O quadrado da medida de um cateto é o produto das medidas da hipotenusa e da projeção ortogonal desse cateto sobre a hipotenusa.”
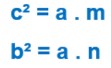
- “O produto das medidas dos catetos é igual ao produto das medidas da hipotenusa e da altura relativa a ela.”
Exemplo do uso das relações métricas
Para você entender melhor vamos mostrar um exemplo do uso dessas relações. Vamos aplicar as relações métricas para descobrirmos os valores numéricos de a, b, c e h:
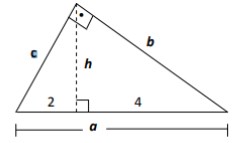
Nesse tipo de situação, temos que listar os dados que já temos que são:
m = 2
n = 4
Observe o triângulo e veja que a hipotenusa a é a soma de n com m, então:
a = n + m
a = 2 + 4
a = 6
O lado maior do triângulo é a hipotenusa e neste caso vale 6.
Com o valor da hipotenusa a e os valores das projeções m e n, podemos calcular facilmente os catetos b e c:
Após fatorarmos o número 24, temos:
Um dos catetos já está calculado, agora falta o outro:
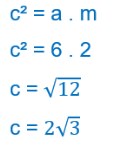
Prontinho! Agora para calcular a altura do triângulo é só usar a expressão:
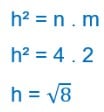
Fatorando o número 8, temos:
Então, concluímos que as relações métricas são utilizadas para descobrir uma ou mais medidas em um triângulo retângulo.
Exercícios resolvidos do Triângulo Retângulo
Com isso, terminamos essa aula, com certeza que você entendeu a importância de estudar sobre os triângulos retângulos. Pratique e detone na prova! Agora é com você!
Referências Bibliográficas:
MATSUBARA, Juliane B. Obra coletiva. Conexões com a Matemática. Vol1. 1ª ed. São Paulo: Moderna, 2010.
MORI, Iracema. Matemática: Ideias e desafios. 9º ano. 15ª ed. São Paulo: Saraiva, 2009
Exercícios
.
Sobre o(a) autor(a):
Wania Maria de A. Pereira - A professora Wania Maria de A. Pereira é graduada em Física e Matemática pela Universidade Federal de Santa Maria (UFSM) e é Psicopedagoga com enfoque em Gestão de Pessoas (UNC) e especialista em Educação a Distância (SENAC- SC). Atuou na rede particular, estadual e municipal por 26 anos no Estado de Santa Catarina. Autora de diversos materiais didáticos para universidades públicas e privadas na área de Matemática, Metodologia de Ensino de Matemática e Psicopedagogia. Atualmente trabalha na área de Projetos de Tecnologias Digitais de Informação e Comunicação (TDICs). LinkedIn: https://www.linkedin.com/in/wmariaap/.
