Relações trigonométricas do triângulo retângulo
A descoberta da relações trigonométricas do triângulo retângulo deu início aos estudos da trigonometria. Aprenda sobre esse assunto no Curso Enem Gratuito e teste seus conhecimentos com a nossa lista de exercícios!
Sabemos que triângulo retângulo é uma referência nas aplicações que envolvem a geometria plana. Em algumas profissões ficaria difícil entender diferentes fenômenos se não usássemos suas diferentes aplicações.
Seu ângulo reto, suas relações métricas e trigonométricas dão ferramentas para cálculos de distâncias muito grandes como entre dois planetas, por exemplo. Sendo assim, você precisar saber tudo sobre as relações trigonométricas do triângulo retângulo.
Relações trigonométricas do triângulo retângulo
Para estudar as relações métricas do triângulo retângulo, é importante lembrar que além de ter um ângulo reto, o seus lados têm nomes específicos que os outros triângulos não têm.
Por ser um tipo especial de triângulo, a literatura especializada dedica capítulos inteiros a seu estudo, pois essa figura é o pilar dos estudos da trigonometria.
Os triângulos retângulos têm dois tipos de relações envolvendo lados e ou ângulos. Essas relações são: as Métricas e as Trigonométricas.
Nosso interesse é o estudo das relações trigonométricas que são usadas quando surgem cálculos entre as medidas dos lados e ângulos de um triângulo retângulo. São conhecidas como seno, cosseno e tangente.
Como calcular
Observe o triângulo retângulo abaixo:
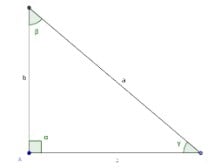
Temos os lados:
a: hipotenusa
b: cateto
c: cateto
E também temos os ângulos α, β e γ.
A relação de seno de um ângulo é dada pela razão entre o cateto oposto do ângulo considerado é a medida da hipotenusa do triângulo. Lembramos que a palavra razão nos remete a uma divisão ou uma fração.
Para definirmos o seno devemos ver qual o ângulo a ser usado e qual é o cateto (lado) que fica do lado oposto a esse ângulo:
Se considerarmos o ângulo β, por exemplo, e usando o conceito de seno temos a seguinte expressão:

Mas se considerarmos o ângulo γ, temos:

A relação de cosseno de um ângulo é dada pela razão entre o cateto adjacente ao ângulo e a medida da hipotenusa do triângulo.
Para o ângulo β, o cateto adjacente b, então:

Logo para o ângulo γ, temos:

Já, a tangente de um ângulo considerado é dada pela razão entre o cateto oposto e o cateto adjacente.
Para o ângulo β, ficamos com:

E para o ângulo γ:

Podemos concluir que os valores das tangentes dos dois ângulos são valores inversos.
Aplicações das relações trigonométricas
As relações trigonométricas são utilizadas para cálculos de distâncias na agrimensura e astronomia.
Também são utilizadas por engenheiros nos projetos de construção civil pois os triângulos por si só são estáveis e muito rígidos evitando deformações nos projetos em andamento.
Na Física as aplicações das relações trigonométricas são infinitas. Como, por exemplo, nos estudos de lançamentos oblíquos, cálculo de tensões na estática de corpos rígidos, no estudo de sistema de forças entre tantos outros assuntos.
Sendo assim, podemos perceber que as relações trigonométricas dos triângulos retângulos são aplicáveis em diversas áreas.
Exercício resolvido
Agora que você já revisou a teoria, vamos a um exemplo de aplicação sobre esse assunto que adora aparecer no Vestibular e no Enem!
1) Uma escada está apoiada em um muro de 2m de altura, formando um ângulo de 45º. Forma-se, portanto, um triângulo retângulo isósceles. Qual é o comprimento da escada?
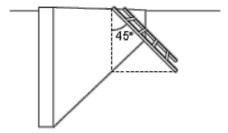
Resolução:
Lendo o enunciado achamos um dado importante: o triângulo retângulo tem um ângulo formado com a parede de 45º. O ângulo reto formado nesse triângulo é entre a parede e a projeção da escada. Logo o ângulo formado entre a escada e o chão também é de 45º.
Veja o esboço abaixo:
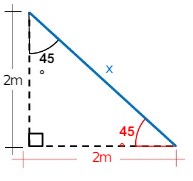
Como o triângulo é isósceles temos dois lados iguais e esses lados são aqueles que formam os ângulos de 90º.
Precisamos então calcular a hipotenusa desse triângulo, através do seno do ângulo de 45º:
![]()
O cateto oposto ao ângulo de 45º mede 2m e a hipotenusa não sabemos.
O sen45º pela tabela trigonométrica é igual a ![]()
Vamos substituir esses dados na fórmula do seno:
![]()
Multiplicando em xis, temos:
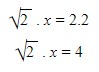
Passando ![]() para o outro lado da igualdade, dividindo 4:
para o outro lado da igualdade, dividindo 4:
![]()
Não podemos deixar a ![]() como denominador, então vamos racionalizar, isto é, multiplicamos a fração toda por
como denominador, então vamos racionalizar, isto é, multiplicamos a fração toda por ![]()
![]()
E, chegamos ao resultado:
![]()
Como ![]() então o comprimento da escada é aproximadamente 2,84 m.
então o comprimento da escada é aproximadamente 2,84 m.
(Fonte: https://goo.gl/9mfHqk)
Resumo sobre as relações trigonométricas
Assista à videoaula a seguir, em que o professor Lucas faz um resumo sobre as relações trigonométricas do triângulo retângulo! A aula também está disponível no canal do Curso Enem Gratuito no YouTube.
Exercícios
Para finalizar seus estudos, resolva os exercícios sobre as relações trigonométricas do triângulo retângulo a seguir!
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(Matsubara, 2017, pg. 317 – adaptado)
No triângulo ABC, com ângulo reto em C, o cateto oposto ao vértice A mede 8 cm e a hipotenusa mede 12 cm. O seno em A desse triângulo é igual a:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre relações trigonométricas do triângulo retângulo para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(Matsubara, 2017, pg. 319 – adaptado)
Um foguete foi lançado formando com o solo um ângulo de 45 graus. Depois de percorrer 1 000 m em linha reta , a que altura estava do chão? ( sem 45 = cos 45 = 0,707, tg 45 = 1)
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre relações trigonométricas do triângulo retângulo para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(Matsubara, 2017, pg. 319 – adaptado)
Uma das extremidades de um cabo de aço está presa a um poste, formando com este um ângulo de 30 graus, enquanto a outra extremidade está fixada no chão a 5 m do pé do poste. A medida do comprimento do cabo de aço e da altura do poste são respectivamente: (Dado: sem 30 = 0,5, cos30 = 0,866, tg 30 = 0,577)
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre relações trigonométricas do triângulo retângulo para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(Questão própria)
Uma escada de 8 m de comprimento está encostada em uma parede. A distância entre o pé da escada e a parede é de 4 m. O ângulo formado entre a escada e a parede é:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre relações trigonométricas do triângulo retângulo para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(UNESP)
Uma pessoa a nível do solo, observa o ponto mais alto de uma torre vertical, à sua frente, sob um ângulo de 30 graus. Aproximando-se 40 metros da torre, ela passa a ver esse ponto sob um ângulo de 45 graus.
A altura da torre em metros é:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre relações trigonométricas do triângulo retângulo para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(Cesgranrio)
Uma escada de 2m de comprimento está apoiada no chão e em uma parede vertical. Se a escada faz 30° com a horizontal, a distância do topo da escada ao chão é de:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre relações trigonométricas do triângulo retângulo para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(UFPE)
A rampa de acesso à garagem de um edifício sobre um terreno plano tem forma retangular e determina um ângulo de 60° com o solo. Sabendo-se que ao meio-dia a sombra da rampa tem área igual a 36 metros quadrados, a área da rampa é igual a:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre relações trigonométricas do triângulo retângulo para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(UFES)
Quatro pequenas cidades A, B, C e D estão situadas em uma planície. A cidade D dista igualmente 50km das cidades A, B e C. Se a cidade C dista 100km da cidade A e 50km da cidade B, qual dos valores abaixo melhor representa a distância da cidade A à cidade B?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre relações trigonométricas do triângulo retângulo para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(Fuvest)
Os vértices de um triângulo ABC, no plano cartesiano, são: A=(1,0), B=(0,1) e C=(0,Ë3). Então, o ângulo BÂC mede:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre relações trigonométricas do triângulo retângulo para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(Unicamp – adaptada)
Caminhando em linha reta ao longo de uma praia, um banhista vai de um ponto A a um ponto B, cobrindo a distancia AB=1.200 metros. Quando em A ele avista um navio parado em N de tal maneira que o ângulo NAB é de 60°; e quando em B, verifica que o ângulo NBA é de 45°. A distância a que se encontra o navio da praia é aproximadamente:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre relações trigonométricas do triângulo retângulo para acertar na hora da prova!

Sobre o(a) autor(a):
Wania Maria de A. Pereira - A professora Wania Maria de A. Pereira é graduada em Física e Matemática pela Universidade Federal de Santa Maria (UFSM) e é Psicopedagoga com enfoque em Gestão de Pessoas (UNC) e especialista em Educação a Distância (SENAC- SC). Atuou na rede particular, estadual e municipal por 26 anos no Estado de Santa Catarina. Autora de diversos materiais didáticos para universidades públicas e privadas na área de Matemática, Metodologia de Ensino de Matemática e Psicopedagogia. Atualmente trabalha na área de Projetos de Tecnologias Digitais de Informação e Comunicação (TDICs). LinkedIn: https://www.linkedin.com/in/wmariaap/.
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


