Gráfico da função logarítmica: matemática Enem
Você já vem estudando matemática há um tempo para as provas de vestibular e Enem. Então, já deve ter se deparado com os mais variados tipos de gráficos. Não é por menos! As provas costumam trazer bastante questões dessa forma. Vem comigo conhecer mais um tipo de gráfico: o gráfico da função logarítmica!
Saber interpretar um gráfico é uma das partes mais divertidas da matemática! Um gráfico não é somente uma reta ou uma curva em um plano, é um compilado de informações que podem ser representados por uma função.
Muitas vezes, só de se observar um gráfico já se consegue coletar dados referentes a um problema (ou uma solução!). Nesta aula você vai ver como se comporta o gráfico da função logarítmica e o que ele pode representar.
Além disso, você vai conseguir interpretar uma função visualmente, o que facilita e agiliza a resolução dos exercícios. Bora começar pela revisão do básico, antes de entrar nos gráficos.
Introdução aos Logarítmos
Veja agora com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito, uma introduçãobásica sobre os Logaritmos.
Daqui a pouco, logo abaixo, confira com o professor Lucas Borguezan as dicas para resoler as questões que mais caem. de matemática Lucas Borguezan um resumo rápido para você revisar o básico sobre os Logarítmos.
Função logarítmica
Para falar sobre o gráfico da função logarítmica, você só precisa relembrar de como ela se apresenta. A função logarítmica é uma função definida por![]() Sendo a base a um número real, positivo e diferente de 1.
Sendo a base a um número real, positivo e diferente de 1.
Além disso, essa função é a inversa da função exponencial, e isso pode ser visualizado na construção do gráfico também
Gráfico da Função Logarítmica
Para construir e interpretar um gráfico de função logarítmica, basta atribuirmos valores a X e calcularmos seu valor em Y, marcando no plano cartesiano os pontos que constituem este gráfico.
Vamos ver por meio de um exemplo como se dá essa construção.
Exemplo: Construa o gráfico cartesiano da função![]()
Solução: Como acabamos de ver, para construir o gráfico para uma função logarítmica, primeiro você dá valores ao X. Em seguida, calcula o Y. Ou vice-versa. Assim, inicialmente daremos valores a Y e depois calculamos X. Veja na tabela a seguir:
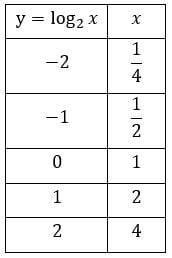
Quanto maior a quantidade de valores para y que você atribuir, mais preciso ficará o esboço do seu gráfico.
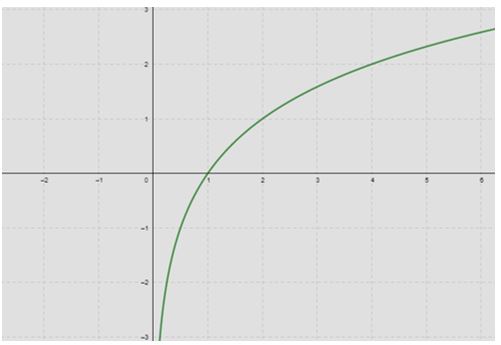
A partir deste exemplo, vamos considerar algumas questões com relação à construção do gráfico da função logarítmica.
Aprenda a resolver Logaritmos
Veja agora com o professor Lucas Borguezan as dicas rápidas para gabritar nas questões de logaritmos.
Propriedades do gráfico da função logarítmica
1- O gráfico sempre estará todo à direita do eixo ![]() .
.
2- Corta o eixo no ponto de abcissa 1 ![]()
Importante: Essas questões são válidas para funções logarítmicas genéricas. Quando existe uma composição de equações, alguns detalhes devem ser observados. Veja os detalhamentos abaixo.
Detalhamento dos tópicos 1 e 2
O gráfico só se encontra à direita do eixo y quando a variável se encontra “sozinha” no logaritmo. Veja o que acontece, por exemplo, se somarmos 3 unidades neste mesmo exemplo:
![]()
O gráfico inteiro se desloca 3 unidades para a esquerda, assumindo então, valores negativos para X, veja:
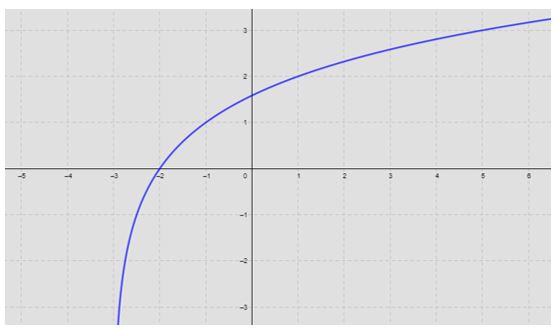
Além disso, o gráfico intercepta (corta) o eixo X no ponto -2.
Da mesma forma, se subtrairmos n unidades do logaritmando, o gráfico desloca-se para a direita.
Exemplo: ![]()
Gráfico:
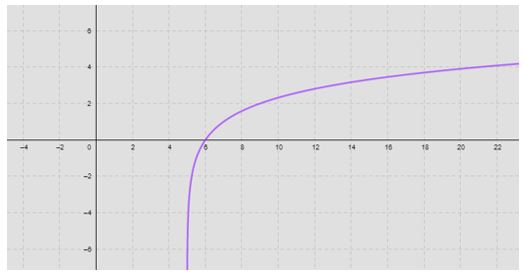
Neste exemplo, o gráfico cortou o eixo X no ponto 6.
Se somarmos ou subtrairmos unidades no logaritmo (e não no logaritmando), o gráfico então se desloca para cima ou para baixo em relação ao eixo .
Exemplo: ![]()
Gráfico:
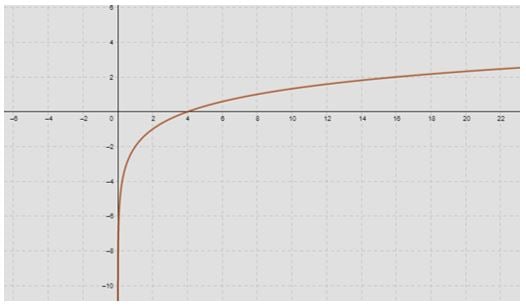
Perceba como, nesse exemplo, o gráfico cortou o eixo X na abcissa de valor 4. O ponto cartesiano que antes era (4, 2) deslocou-se duas unidades para baixo, ocupando o espaço do ponto (4,0).
Nos exemplos apresentados acima, somente verificamos gráficos de funções logarítmicas crescentes, ou seja, quando a > 0 . O que nos leva para a terceira questão que diz:
3- Se a função a > 1 é crescente, e se 0 < a < 1, a função é decrescente.
Vamos construir um gráfico de uma função com ![]() . Para isso, atribuímos valores à função, calculando, em seguida, o valor de x.
. Para isso, atribuímos valores à função, calculando, em seguida, o valor de x.
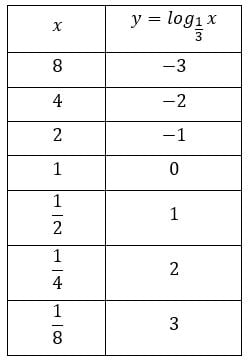
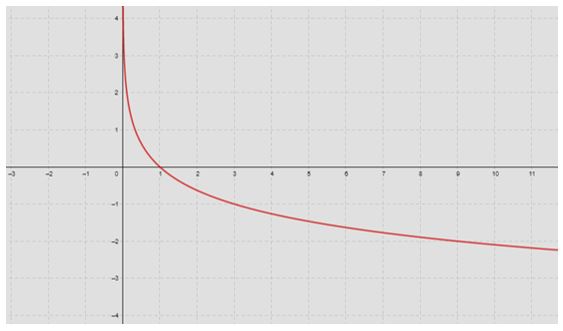
Ao observar o gráfico você percebe que os valores da função são decrescentes de maneira logarítmica. Além disso, todas as propriedades apresentadas anteriormente são equivalentes para o gráfico decrescente. O importante é sempre prestar atenção nas condições de existência e nas propriedades.
A aula de hoje chegou ao fim, mas você ainda tem muito trabalho pela frente. Sugiro que utilize a ferramenta Geogebra para experimentar na prática como se comportam os gráficos das mais variadas funções. A plataforma é bastante intuitiva e vai lhe abrir novos horizontes e interpretações nos estudos.
Exercícios:
Questão 01) As funções logarítmicas f, g, h, p são dadas por f(x) = 10 + log x, g(x) = 10log x, h(x) = log(10x) e p(x) = log(x + 10). Observe os gráficos a seguir:
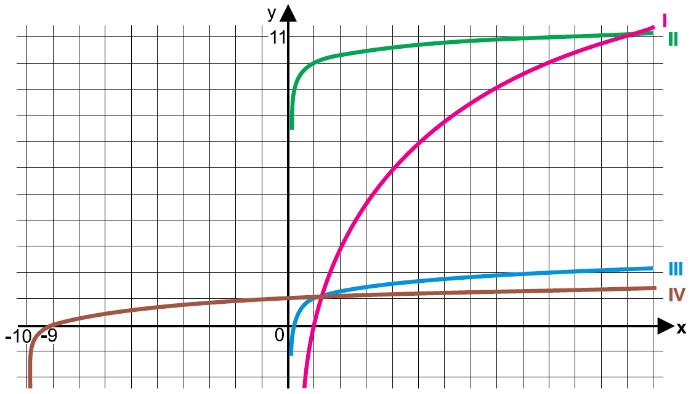
Os gráficos I, II, III e IV correspondem, respectivamente, às funções
a) h, f, g, p.
b) g, h, f, p.
c) g, f, h, p.
d) g, f, p, h.
e) p, f, h, g.
Questão 02) O gráfico a seguir ilustra o processo de eliminação de 10 ml de determinado medicamento injetado em um paciente no instante inicial de observação. Observa-se que, decorridas 2,5 horas, havia 3,7 ml do medicamento no organismo do paciente.
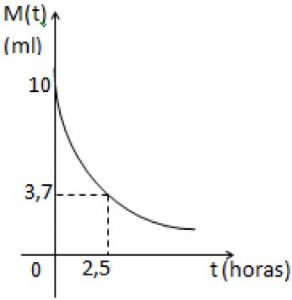
Considerando que a representação analítica para esse gráfico é a função exponencial cuja base é o número de Euler e dada por M(t) = k.e–at, sendo k e a constantes reais, e dados os logaritmos naturais ln 2 = 0,69, ln 5 = 1,61 e ln 0,37 = –1, é CORRETO afirmar que o tempo necessário para que o organismo do paciente retenha 10% da quantidade inicial do medicamento é de
a) 1h 05 min
b) 2h 15 min
c) 3h 25 min
d) 4h 35 min
e) 5h 45 min
Questão 03) A imagem indica o gráfico das funções 1 e 2, ambas definidas para x real e maior do que zero.
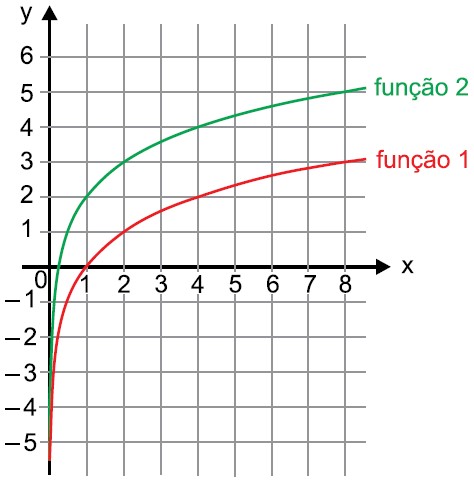
De acordo com o gráfico, as funções 1 e 2 podem ser, respectivamente,
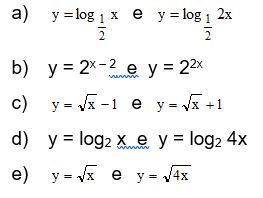
01) Gab: C
02) Gab: E
03) Gab: D





