Área e Perímetro de figuras planas: veja como calcular
A geometria plana e a espacial são assuntos que são bastante cobrados no Enem e nos vestibulares. Para compreendê-los mais tarde é preciso que você tenha em mente alguns dos conceitos básicos do cálculo de área e do perímetro
Calcular perímetro e área foi uma das primeiras preocupações dos povos antigos. Quando começaram a dividir suas terras e segmentar entre áreas de plantio e construções, precisavam ter as medidas do espaço para ninguém “sair perdendo”.
O cálculo de área é um interesse milenar. Iniciou-se com o cálculo da área de figuras geométricas mais simples como, quadrado e retângulo.
Cálculo de área e de perímetro
Conforme o conhecimento era desenvolvido, percebeu-se que poderiam calcular perímetro e área de qualquer figura geométrica. Aliás, a própria palavra geometria significa medida de terra (geo = terra, metria = medida).
Cálculo de perímetro
O cálculo do perímetro nada mais é do que a soma de todos os lados de uma figura geométrica. Ao calcular o perímetro, estamos calculando o contorno de determinada região. É como se passássemos uma linha por todo o comprimento da figura geométrica e depois medíssemos o tamanho da linha.
Exemplo
Qual o perímetro de um campo de futebol que tem base 100 metros e altura 70?
Solução do problema: As medidas expressas no exemplo representam uma região retangular que pode ser representada por: Logo, sendo o perímetro (P) a soma de todos os lados da figura, temos:
Logo, sendo o perímetro (P) a soma de todos os lados da figura, temos:
- P = 100 + 100 + 70 + 70
- P = 340 metros.
O que é o semiperímetro?
Define-se por semiperímetro a medida da metade do perímetro de uma figura geométrica. Costuma ser representada pela letra S. Para calcular o semiperímetro basta calcular o perímetro normalmente e dividir o resultado por 2.
Cálculo da área
Resumo sobre como calcular área de figuras planas
Confira agora com o professor Lucas Borguesan, do canal do curso Enem Gratuito, uma revisão básica:
Você já viu que o cálculo do perímetro é a soma dos lados ou seja, o comprimento do contorno de determinada região. Agora vamos estudar a área, que nada mais é do que o espaço ocupado por esta região.
Área de um retângulo
O cálculo da área (A) de uma região retangular é dada pela multiplicação entre a medida da base (b) (comprimento) e a medida da altura (h) (largura).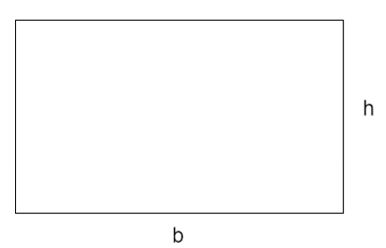 Dado pela fórmula: A = b x h A área é o resultado do cálculoda base vezes a altura.
Dado pela fórmula: A = b x h A área é o resultado do cálculoda base vezes a altura.
Caso especial: O quadrado é um retângulo especial onde a base (b) e a altura (h) possuem o mesmo tamanho, logo chamamos esta medida de lado do quadrado, dessa forma, a fórmula fica:
- A = b h
- A = l l
- ou ainda
- A = l²
Exemplo de cálculo de área
Calcular a área de um quadrado de lado 4m.
A = l l
A = 4m 4m
A = 16 m²
Importante: por se tratar de unidades de medida, é sempre bom colocar a unidade respectiva para fins de identificação. Ao ver uma medida como 16 metros quadrados, você já sabe que se trata de uma medida de área.
Área do triângulo
Se você utilizar sua imaginação, consegue perceber que um triângulo nada mais é do que um retângulo dividido ao meio. E daí vem a surpresa: para calcular a área do triângulo, basta multiplicar a base (b) pela altura (h) e dividir o resultado por 2.
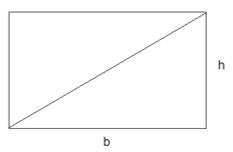
Assim, a fórmula é dada por:
A = (b h) / 2
Importante: nem sempre as medidas da base e da altura serão dadas, às vezes é preciso descobrir essas medidas através dos valores que o problema informa.
Exemplo
Calcular a área do triângulo Equilátero de lado 6 cm.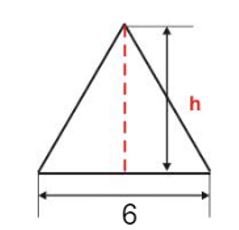 Perceba que neste exemplo você tem o valor dos lados (por ser equilátero, todos os lados tem medida 6 cm) mas o problema não mostra o valor da altura. Nesse caso, utiliza-se o Teorema de Pitágoras para determinar essa medida.
Perceba que neste exemplo você tem o valor dos lados (por ser equilátero, todos os lados tem medida 6 cm) mas o problema não mostra o valor da altura. Nesse caso, utiliza-se o Teorema de Pitágoras para determinar essa medida.
A altura do triângulo equilátero equivale à mediana, ou seja, “corta” o lado em duas partes iguais.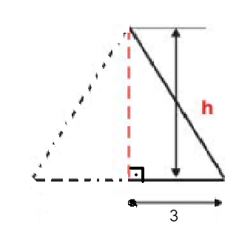
Assim, para calcular a medida da altura basta que: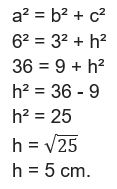
Agora, com a medida da altura (h) podemos calcular a área
A = (b h) / 2
A = (6 5) / 2
A = 30 / 2
A = 15 cm²
Se quiser saber mais sobre o cálculo da área dos triângulos é só dar uma olhadinha nesta videoaula do professor Lucas Borguesan, do Canal do Curso Enem Gratuito!
Área do losango
O losango é uma das figuras geométricas onde para calcular área não se utilizam as medidas dos lados, e sim das diagonais, assim, para calcular a área de um losango basta multiplicar a diagonal maior (D) pela diagonal menor (d), e dividir por 2, resultando na fórmula:
A = (D d) / 2
Exemplo
Calcule a área de um losango cuja diagonal maior é 3 vezes maior do que a diagonal menor e esta mede 7 cm.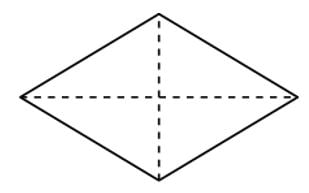 Diagonal menor (d) = 7 cm
Diagonal menor (d) = 7 cm
Diagonal maior (D) = 3 x 7 = 21 cm
A = (Dd) / 2
A = (21 7) / 2
A = 147 / 2
A = 73,5 cm²
Portanto, a área do losango é 73,5 centímetros quadrados.
Exercícios sobre figuras planas
Questão 01)
A figura abaixo mostra um quadrado ABCD que é formado de um quadrado limitado por 4 retângulos iguais. O perímetro de cada retângulo é 60 cm.
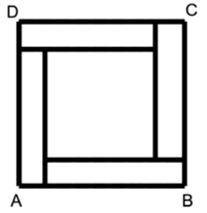
Qual é a área, em cm2, do quadrado ABCD?
a) 600
b) 800
c) 900
d) 950
e) 980
Questão 02)
Uma praça de forma retangular, cujo lado maior mede o dobro do lado menor, tem uma área de 12.800 m2. Ao longo do perímetro dessa praça, foi construída uma pista para caminhadas. Se uma pessoa der exatamente cinco voltas completas nessa pista, percorrerá um total de
a) 2,4 km
b) 2,6 km
c) 2,8 km
d) 3,2 km
e) 3,4 km
Questão 03)
O proprietário de alguns imóveis deseja vender um de seus terrenos para comprar um apartamento. Para que a imobiliária possa publicar o anúncio de venda em seu site, solicita ao proprietário que ele informe quais as dimensões do terreno.
O dono, então, informa que se trata de um terreno retangular com 74 m de perímetro e que o comprimento do imóvel tem 5 m a mais do que sua largura.
Assinale a alternativa CORRETA.
Com base nesses dados, o corretor de imóveis concluiu, de maneira correta, que as dimensões do terreno e sua área são, respectivamente,
a) 18 m, 23 m e 414 m2.
b) 17 m, 22 m e 374 m2.
c) 16 m, 21 m e 336 m2.
d) 15 m, 20 m e 300 m2.
e) 14 m, 19 m e 266 m2.
Questão 04)
Um terreno possui a forma retangular com dimensões iguais a 30 metros de largura por x metros de comprimento. Sabendo-se que sua área é igual a 1200 metros quadrados, qual o perímetro do terreno?
a) 60 metros
b) 70 metros
c) 100 metros
d) 120 metros
e) 140 metros
Gabarito:
- C
- A
- C
- E





