Quadriláteros: veja o que são, os tipos e classificações
A Geometria está por toda a parte: em nossas casas, prédios, campos de futebol, mesas de bilhar, quadras poliesportivas e em muitos outros lugares. Estude os quadriláteros nessa revisão de Matemática do Curso Enem Gratuito!
Às vezes os vestibulares e o Enem propõem questões de Geometria que nos tiram o sossego. Geralmente as mais difíceis são aquelas que trazem a descrição de determinada figura e não tem sua imagem. É comum que essas questões comecem assim:
“(Unicamp) Um trapézio retângulo é um quadrilátero convexo plano que possui dois ângulos retos, um ângulo agudo α e um ângulo obtuso β. Suponha que, em um tal trapézio, a medida de β seja igual a cinco vezes a medida de α. Calcule a medida de α, em graus.”
E a gente lê esse tipo de questão e se pergunta: Por onde eu começo?
Pensando nesse tipo de questão, resolvi fazer uma revisão com você sobre os famosos quadriláteros, aquelas figuras que têm quatro lados com diferentes “nomes e sobrenomes”.
O que são quadriláteros?
Os quadriláteros são figuras geométricas essenciais na geometria. Os quadrados, losangos e retângulos são os mais conhecidos. Porém, existem outros que ganham visibilidade no estudo de áreas e perímetros como os paralelogramos e os trapézios.
Nesta aula vamos apresentar suas características principais para que você possa resolver com tranquilidade as questões do Enem e Vestibular que envolvem essas figuras.
Características gerais dos quadriláteros
O conceito de quadrilátero é simples. Um quadrilátero é um polígono simples de quatro lados.
Temos como exemplos dessas formas os pisos de nossas casas, paredes, camas, mesas, prédios, campos de futebol, partes de uma caixa, faces de um tijolo.

Uma das características importantes dos quadriláteros é que a soma de seus ângulos que é igual a 360º. Outra característica importante de ser lembrada é que os quadriláteros têm duas diagonais.
Resumo sobre os Quadriláteros
Veja agora com o professor Vini, que dá aulas de matemática no canal do Curso Enem Gratuito, as dicas básicas para você ressolver e gabaritar nas questões de Geometria Plano nas provas do Enem:
Tipos de quadriláteros
Existem dois tipos de classificação de quadriláteros: paralelogramos e trapézios.
Vamos estudá-los separadamente:
Paralelogramos
Os paralelogramos são figuras geométricas planas que têm lados opostos paralelos. São quadriláteros convexos.

Propriedades dos paralelogramos:
- Os ângulos opostos são congruentes.
- Os ângulos adjacentes são suplementares (α + β = 180º)
- Os lados opostos são congruentes.
- As diagonais se interceptam nos pontos médios.
Área do paralelogramo
A área dos paralelogramos em geral se calcula através de:
Área = base x altura
Retângulo
Os retângulos são quadriláteros convexos equiângulos. Ou seja, são paralelogramos que têm quatro ângulos iguais a 90º(retos), dois lados opostos menores e dois lados oposto maiores. Tem diagonais congruentes.

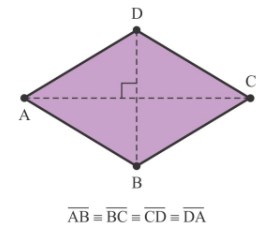
Losango
É um quadrilátero convexo equilátero. Isto quer dizer que é um paralelogramo que tem quatro lados iguais e têm suas diagonais perpendiculares entre si. Suas diagonais dividem o losango em quatro triângulos retângulos.
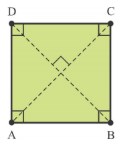
Quadrado
É um quadrilátero convexo, equilátero e equiângulo, isto é, têm quatro lados com medidas iguais e quatro ângulos internos iguais a 90º (ângulos retos). Suas diagonais são perpendiculares entre si, e seu encontro dá seu ponto médio da figura.
Dizemos que o quadrado é um quadrilátero regular e é um retângulo e um losango.
Trapézios
Trapézios são polígonos quadriláteros que têm dois lados paralelos, que são chamados de bases.
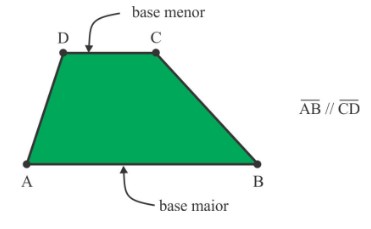
Área do trapézio
Sua área é calculada através da fórmula:
Área = [ (Base maior + Base menor) x altura ] / 2
Classificação dos trapézios
Os trapézios podem ser classificados em isósceles, retângulo ou escaleno.
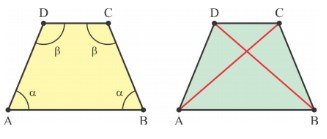
Trapézio Isósceles: essa figura tem seus lados opostos não paralelos congruentes, isto é, têm a mesma medida. Os ângulos de cada base e suas diagonais também são congruentes.
Trapézio Retângulo: um dos lados é perpendicular às bases, ou seja, forma um ângulo de 90º às bases.

Trapézio Escaleno: os lados não paralelos dessa figura não são congruentes, isto é, não tem a mesma medida.
Exercício resolvido
Agora que já sabemos as diferenças entre os quadriláteros podemos com facilidade resolver a questão da Unicamp:
Um trapézio retângulo é um quadrilátero convexo plano que possui dois ângulos retos, um ângulo agudo α e um ângulo obtuso β. Suponha que, em um tal trapézio, a medida de β seja igual a cinco vezes a medida de α.
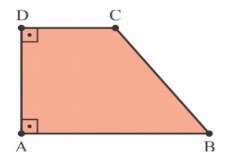
Calcule a medida de α, em graus.
Resolução: a soma das medidas dos quatro ângulos é 360º e o enunciado diz que β = 5α. Vamos calcular a medida de α:
α + β + 90 + 90 = 360
α + β + 180 = 360
Substituindo β por 5α na equação:
α + 5α = 360 – 180
6α = 180
α = 30
E a questão está resolvida!
Como você pode perceber, cada quadrilátero tem suas características e você sabendo suas diferenças vai acertar todas as questões que os envolvem.
Referências Bibliográficas
- ANTIGO, Edilene A. D. A Aprendizagem do Conceito de Quadriláteros por meio d Resolução de Problemas. UEM, 2014. Disponível em: https://goo.gl/aMGLr7.
- Quadriláteros Convexos_ UNICAMP. Disponível em: https://goo.gl/fdrtiW. Acesso em 22/12/2018.
Resumo sobre os Polígonos
Aprenda mais sobre polígonos e geometria plana com o professor Sérgio Sarkis, de Matemática, assistindo à videoaula abaixo!
Exercícios sobre quadriláteros
.