Veja o que é a Força Resultante e como ela se distribui no plano horizontal e no plano inclinado. Veja como fazer o cálculo das forças que atuam sobre um determinado corpo para encontrar a Resultante de Forças, com a Grandeza vetorial, seu módulo, direção, e sentido.
Nesta aula de Física você vai aprender o que é e quais as características da resultante de duas ou mais forças no plano horizontal e no plano inclinado.
Você vai aprender ainda a identificá-las sempre como grandezas vetoriais e em seguida saberá calcular a aceleração de blocos em movimento na direção horizontal e inclinada. Vem com a gente e se prepare para mandar em Física no Enem e nos vestibulares com a força resultante!
O primeiro passo para começar esta revisão é ver um resumo com a professora Lia, que dá aulas de Física no canal do Curso Enem Gratuito, com todas as dicas sobre a Força Resultante.
Força Resultante
Um corpo pode estar submetido a forças que atuam nele em diferentes direções e sentidos. Para compreender os efeitos de um grupo de forças que atuam em um corpo, é mais fácil tratarmos todas as forças como uma única força. Esta força será o resultado da soma de todas envolvidas.
Essa única força denominamos de “Força Resultante” ou “Resultante das Forças”. Como é uma grandeza vetorial, devemos sempre observar seu módulo, direção e sentido.
Forças na mesma direção

A – Quando elas tiverem mesmo sentido, a Resultante delas será a soma das duas:

B – Quando elas tiverem sentidos opostos, a Resultante será obtida pela subtração da menor pela maior e seu sentido será o da força maior:
Forças em direções perpendiculares, conhecido também ortogonais

A resultante das forças será obtida usando o Teorema de Pitágoras e o sentido será aquele da soma realizada através do método do paralelogramo ou da poligonal.

Para todos os demais ângulos formados entre duas Forças, inclusive 90o, a Resultante será obtida pela lei dos cossenos para Resultantes e o sentido será dado pela regra do paralelogramo ou da poligonal como mostrada no caso anterior.
Força resultante no plano horizontal com cálculo da aceleração
Utilizaremos dois exemplos, o primeiro sem atrito e o segundo com atrito. Vamos lá?

Exemplo 1
No bloco da figura estão representadas duas Forças que agem sobre ele. Admita que o bloco possui massa de 2kg.
Considere que tem intensidade F1 de 3,5N e F2 1N. Vamos calcular a aceleração do bloco:
Como as Forças têm mesma direção e sentidos opostos, o cálculo da resultante fica:
Fr = 3,5 – 1
Fr = 2,5N
Para calcular a aceleração, fazemos uso da segunda lei de Newton Fr = m.a
2,5 = 2.a
a = 2,5
a = 2,5/2
Resultado: aceleração = 1,25 m/s2
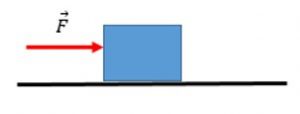
Exemplo 2
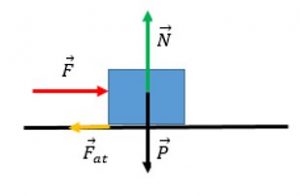
Agora vamos ver um exemplo onde o atrito é levado em consideração. No bloco abaixo está representado um força de 20N e sua massa é 4kg. Entre a superfície e o bloco existe atrito cujo coeficiente vale 0,3. Utilize para aceleração da gravidade 10m/s2. Calcule a aceleração do bloco.
Primeiramente iremos identificar as forças envolvidas: vamos calcular a força peso e, ao mesmo tempo, saberemos o valor da força normal:
P = m . g
P = 4.10
P = 40N
Então, a força normal também será 40N. Agora calculamos a força de atrito cuja fórmula já vimos em outro post que é:
Fat = μ . N
Fat = 0,3.40
Fat = 12N
Agora calculamos a aceleração utilizando a segunda lei de Newton, mas com o incremento do atrito:
F – Fat = m . a
20 – 12 = 4.a
8 = 4.a
4.a = 8
a = 8/4
Resultado: a = 2 m/s2
Percebeu que fomos passo a passo? Fazendo assim você consegue prestar atenção a todos os detalhes. Não dê bobeira!
Resumo sobre a Força de Atrito
Confira agora com o professor de física Antônio Martins, o Tonho, do canal do Curso Enem Gratuito, as dicas básicas para você calcular a Força Resultante com o componente da Força de Atrito:
Força resultante no plano inclinado com cálculo da aceleração
Aqui, mais do que nunca, é necessário irmos devagar e estarmos atentos à todos os detalhes envolvidos. Veja porquê:
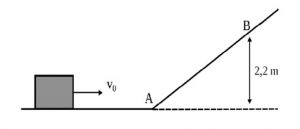
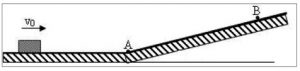
Um plano inclinado consiste em uma superfície plana com uma inclinação em relação a horizontal dada por um ângulo. Observe a figura:
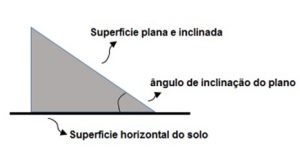
Antes de começar os exemplos, precisamos relembrar de alguns detalhes:
- A força Peso é e sempre será vertical e com sentido para baixo;
- A força Normal sempre será perpendicular a superfície de contato;
- A força de Atrito sempre terá sentido oposto ao movimento.
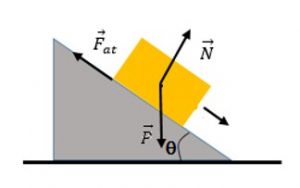
Agora, acompanhe:
Para obtermos a aceleração em rampa inclinada, precisamos decompor a força peso na direção de deslocamento do bloco. Também podemos calcular a força de Atrito (paralela à rampa) e, na direção perpendicular à rampa, calculamos a força Normal.
Notas:
- θ1 e θ2 são iguais, isto é, possuem o mesmo valor.
- Px representará a força Peso decomposta na direção do deslocamento, enquanto Py na direção perpendicular a superfície de contato. Veja na figura suas representações:
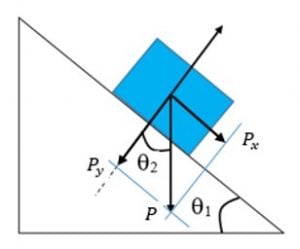
- Px será calculado através do seno do ângulo θ1, pois tem o mesmo comprimento do cateto oposto a θ2, isto é: Px = P. sen θ1.
- Py será calculado usando o cosseno do ângulo θ1, pois equivale ao cateto adjacente do ângulo θ2, isto é: Py = P. cos θ1.
- Lembre-se que Py = N, por isso que calculamos ele.
Resumo sobre o Plano Inclinado
Antes de acompanhar a resolução de exercícios de Plano Inclinado, confira a revisão com o professor Marcelo Alves, do canal do Curso Enem Gratuito:
Exercícios de plano inclinado
Agora, vamos a um exemplo para resolveremos tudo passo a passo:
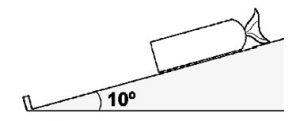
A rampa abaixo possui inclinação de 51o e sobre ela desliza uma caixa de massa de 5 kg. Admita que o coeficiente de atrito entre a superfície da rampa e a base da caixa seja 0,2 e utilize g = 10 m/s2.
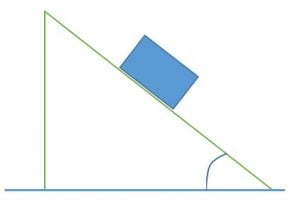
Primeiramente, desenhe todas as Forças envolvidas e determine com qual aceleração a caixa se movimenta.
Resolução:
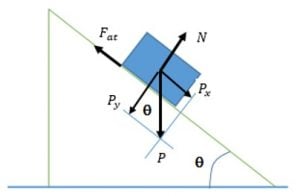
Desenhando os vetores das Forças envolvidas:
Passos para o cálculo da aceleração:
- Calculamos a força Peso;
- Depois calculamos Px e Py;
- Calculamos a força de atrito;
- Por fim, calculamos a aceleração através da segunda lei de Newton. Lembre-se de que a Força utilizada na fórmula é aquela que gera o movimento, isto é, o Px.
Vamos lá, então, para o segundo passo:
- 1º Força Peso: P = m . a
- P = 5.10
- P = 50 N

2º Px e Py: Px = P. senθ e Py = P. cosθ
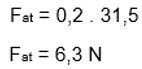
3º Força de Atrito: Fat = μ . N Lembre que a Força Normal é igual a Py:

4º Enfim, calculamos a aceleração pela segunda lei de Newton onde F é o Px:
Interpretando essa questão, podemos perceber que a caixa desce a rampa com aceleração de 6,5 m/s2. Como utilizamos os valores aproximados para seno e cosseno, o valor da aceleração calculada também é aproximado.
Viu como fazer tudo detalhadamente torna mais fácil resolver questões de força resultante?
Videoaula
Para terminar, assista à videoaula abaixo, com a professora Lia!
Exercícios sobre força resultante
Agora resolva os exercícios sobre força resultante selecionados pela equipe do Curso Enem Gratuito!
.