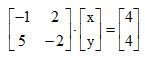Saber somar, multiplicar, fazer matriz transposta e matriz inversa é um passo importante para mandar bem na prova de Matemática do Enem e vestibulares. Aprenda agora, com aula gratuita, dicas, e exercícios resolvidos.
Os cálculos envolvidos nas operações com matrizes e entre matrizes estão diretamente ligados a tudo que você vem aprendendo em matemática desde o ensino fundamental. É preciso e necessário aplicar os conhecimentos em somas, subtração, multiplicação, operações com frações, sistema de equações, e tudo isso agregado às novas informações sobre operações com as matrizes.
Operações com matrizes
Vamos agora abordar cada tipo de operações com matrizes e as propriedades de cada uma.
Matriz oposta
Você lembra que o oposto de um número é o próprio número com o sinal “trocado”? Bom, com as matrizes não é diferente. A oposta de uma matriz possui os mesmos elementos da matriz só que com o sinal invertido, sendo então, .
Exemplo
Qual a oposta da matriz
Solução: Sendo que para definir a oposta de uma matriz basta inverter os sinais de cada um dos termos da matriz, temos que a oposta de A é: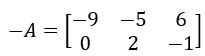
Matriz transposta
Apesar do nome parecido, a matriz transposta é bem diferente da matriz oposta. A matriz transposta nada mais é do que a matriz que resulta quando transformamos as linhas em colunas em uma matriz, sempre mantendo a ordem em que os termos nela aparecem. A transposta de uma matriz é denotada por At.
Exemplo
Assim, utilizando a mesma matriz do exemplo de matriz oposta, temos que a transposta de
É dada por: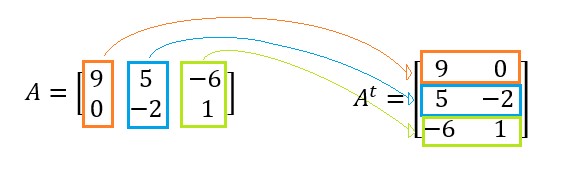
Perceba que a matriz A3×2 transformou-se em uma matriz A2×3. Isso é algo bem importante para ser levado em consideração ao calcular a transposta de uma matriz. Por definição, a matriz Amxn admite uma transposta da forma Anxm.
Propriedades da simetria de matrizes
- Uma matriz é simétrica, se, e somente se, ela for igual à sua transposta A=At
- Uma matriz é antissimétrica, se, e somente se, ela for igual à oposta de sua transposta: A=-At.
Igualdade de matrizes
Essa é fácil, vai? Duas matrizes serão iguais se e somente se, possuírem a mesma ordem e todos os seus elementos forem iguais, ou seja
Exemplo
Se A e B são matrizes iguais, então calcule x;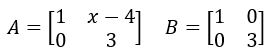
Solução: Bem, se as matrizes são iguais, todos os seus termos são iguais. Assim, temos: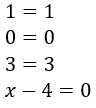
Então é só calcular o valor de x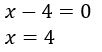
Soma e subtração de matrizes
A única condição necessária para somar duas matrizes é que as duas sejam de mesma ordem, independentemente se for matriz quadrada ou não. Sendo assim, uma matriz da forma Amxn pode ser somada a uma matriz da forma Bmxn resultando em uma matriz Cmxn, onde cada elemento cji da matriz C é igual à soma dos elementos aji e bji de A e B.
Exemplo
Dadas as matrizes A e B, encontre C onde C = A + B.
Organizamos as matrizes em notação de soma: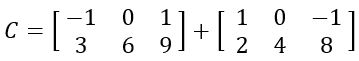
Em seguida, somamos termo a termo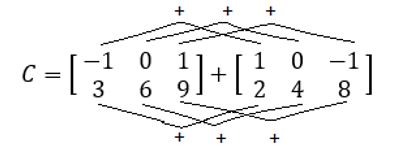
Tome cuidado com os sinais…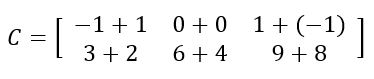
O resultado é da forma: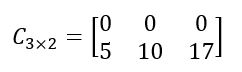
Já a subtração se dá da mesma forma, subtraindo termo a termo. Por definição, dizemos que a subtração entre duas matrizes de mesma ordem é obtida a partir da soma da matriz A com a oposta de B, assim A – B = A + (-B).
Resumo de Soma e Multiplicação de Matrizes
Confira agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, uma explicação simples e rápida para você gabaritar em questões de Soma e Multiplicação de Matrizes.
Valeu pra você o resumo do professor Lucas? Veja agora os exemplos de multiplicação de matrizes.
Multiplicação de um escalar por uma matriz
Para multiplicar um número real por uma matriz também não tem muito mistério, basta multiplicar o número em questão por cada termo da matriz individualmente. Veja o exemplo.
Exemplo
Multiplique o número k = 3 pela matriz
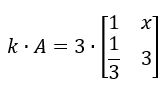
Multiplicando termo a termo:
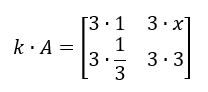
O resultado é a matriz:
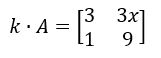
Multiplicação de uma matriz por outra matriz
Para efetuar a multiplicação entre duas matrizes, existe uma condição onde o produto A x B só pode ser obtido se o número de colunas de A for igual ao número de linhas de B. A matriz resultante terá como ordem o número de linhas de A e o número de colunas de B. Assim,
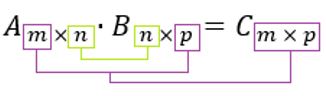
Mas, como é de fato executada essa multiplicação? Basta multiplicar termo a termo? A resposta é não! O produto entre duas matrizes A e B é a matriz C, em que cada elemento é a soma dos produtos de cada elemento da linha de A pelo elemento correspondente da coluna de B. Veja isso na prática com o exemplo abaixo.
Exemplo
Sejam as matrizes A e B, determine C = A . B
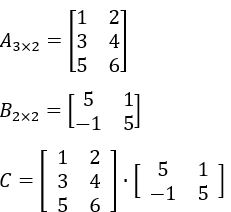
Fazendo a soma dos produtos de cada elemento da primeira linha de A com a primeira coluna de B, temos:
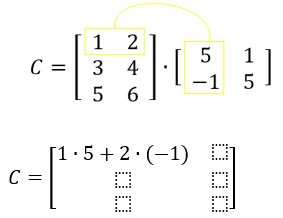
Agora, a soma dos produtos de cada elemento da primeira linha de A com a segunda coluna de B, temos
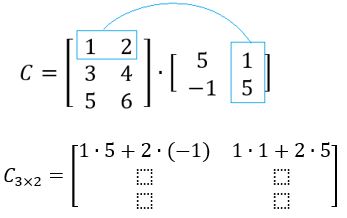
E assim sucessivamente, até efetuarmos as operações entre todos os termos de todas as linhas e colunas,
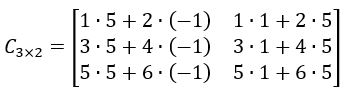
O que resulta em:
Um detalhe importante a ser considerado é que o elemento neutro da multiplicação entre matrizes é a matriz identidade In.
Por isso a matriz identidade também é utilizada no cálculo da matriz Inversa. Veja o tópico a seguir.
Matriz inversa
Para encontrar a inversa X de uma matriz A dada, devemos solucionar a igualdade de matrizes:
Onde A é a matriz dada, A-1 é a matriz inversa e In é a matriz identidade. Além disso, somente matrizes quadradas possuem inversa.
Importante: se o determinante de uma matriz for igual a zero, essa matriz não possui inversa.
Vejamos por meio de um exemplo numérico como se dá o cálculo.
Exemplo
Determine a inversa da matriz A:
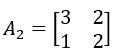
Organizando a igualdade de matrizes, temos:
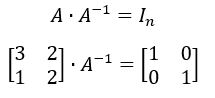
Mas, se não temos a inversa ainda, como efetuar essa multiplicação?
Bem, vamos “criar” uma matriz inversa, onde os seus elementos serão letras, assim:
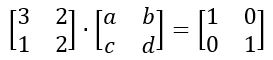
Agora, basta utilizar os conhecimentos de multiplicação de matrizes para efetuar os cálculos, resultando em um sistema de equações com duas incógnitas, veja:
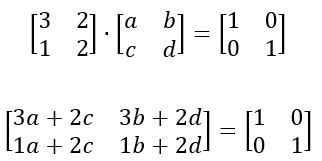
Agora, organizando em sistemas de equações, temos:
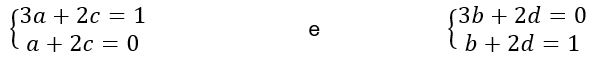
Resolvendo os sistemas, temos que
Assim, a inversa A-1 de A é:
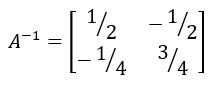
Veja uma dica para o próximo conteúdo sobre Matries, que é o Cálculo do Determinante:
Exercícios sobre operações com matrizes
.
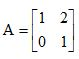satisfaz a equação A2 = aA + bI, em que I é a matriz identidade de ordem 2. Logo, o produto ab é igual a
, com 
, 
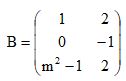e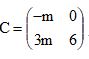 
, sendo m um número real. Sabendo que C = AB, então det C é igual a
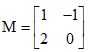e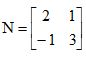 
, então MNT – M–1 N é igual a
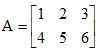e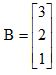 
, o elemento c11 da matriz C = AB é
