A probabilidade condicional é a probabilidade de um evento ocorrer estando condicionado a outro. Os exercícios sobre probabilidade que costumam cair na prova do Enem e vestibulares nem sempre são um bicho de sete cabeças.
A probabilidade condicional é um ramo do estudo da ocorrência de eventos em um espaço amostral. Nesse espaço, é levado em consideração um evento já ocorrido para o cálculo da probabilidade de ocorrer outro evento relacionado ao primeiro. O assunto é fácil, mas esse tanto de palavras difíceis muitas vezes faz com que o aluno creia que o conceito é mais difícil do que realmente é.
A verdade é que mesmo no aprendizado de matemática precisamos utilizar a interpretação de texto a nosso favor. A partir do momento que você souber interpretar um problema ele se torna facilmente solucionável. Veja nessa aula a explicação para exemplos que costumam confundir a cabeça do vestibulando.
O que é probabilidade
Revisando um pouco o que é a probabilidade, podemos dizer que é o cálculo das possibilidades de um evento ocorrer a partir de um experimento aleatório realizado em um espaço amostral. O espaço amostral é dado por n(s) e são todas as possibilidades dadas por um experimento. Podemos citar como exemplo o lançamento de um dado: como o dado tem 6 faces enumeradas de 1 a 6, dizemos que o espaço amostral do lançamento é n(s) = 6.
A possibilidade de um evento ocorrer dentro deste espaço amostral, é determinada por um enunciado.
Exemplo: Ao lançarmos um dado qual a probabilidade de sair um número par?
Bem, levando em consideração que os números pares em um dado são {2, 4, 6}, temos 3 possibilidades em 6 elementos do espaço amostral, logo a probabilidade de sair um número par é
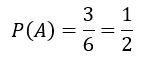
O que é probabilidade condicional
A probabilidade condicional como o próprio nome diz, é a probabilidade de um evento ocorrer estando condicionado a outro. Nesses casos, é necessário que haja uma relação entre os dois eventos e que os eventos sejam conjuntos não vazios. Em outras palavras, podemos dizer que a probabilidade condicional é a probabilidade de um evento A ocorrer sabendo que já ocorreu outro evento B.
A probabilidade condicional é dada pela fórmula:

Com P(B) ≠ 0.
Importante: o cálculo da probabilidade condicional só é possível quando os eventos forem dependentes entre si. Se os eventos forem independentes, a probabilidade do evento A em relação ao evento B não se altera.
Um bom exemplo de evento dependente são as cartas de um baralho. As cartas de um baralho devem, necessariamente, ter um número e um naipe.
Exemplo: Ao escolher aleatoriamente uma carta em um baralho comum de 52 cartas, qual a probabilidade de sair uma rainha sabendo que é uma carta de espadas?
Bom, nesse exemplo percebemos que a carta escolhida tem uma condição: está condicionada a ser de espadas. Então, calculando as probabilidades separadamente, temos:
A = rainha
B = espadas
Já que são 4 rainhas em um baralho comum a probabilidade de sair uma rainha é de

Seguindo a mesma linha de raciocínio, a probabilidade de sair uma carta de espadas é de
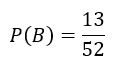
Se pensarmos na intersecção entre os dois conjuntos e levarmos em consideração que só é possível ter 1 rainha de espadas em um baralho de 52 cartas, temos que
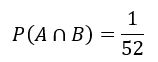
Aplicando a fórmula da probabilidade condicional, temos:
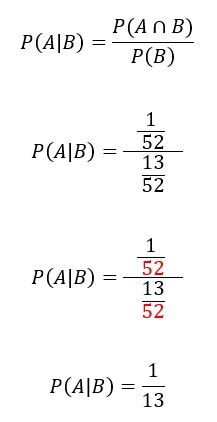
Então, a probabilidade de sair uma rainha de espadas é de ![]() .
.
Exemplo de probabilidade condicional
Muitas vezes não é necessário aplicar fórmulas para obter o resultado, na verdade, para a probabilidade condicional você pode efetuar os cálculos reduzindo o espaço amostral. Veja:
Exemplo: Em um jogo de RPG, ao se lançar o dado que possui 20 faces, percebeu-se que o número é maior que 11. Qual a probabilidade de ser um número múltiplo de 4?
Bom, o espaço amostral no início da questão é de 20 elementos (todas as faces do dado), porém, já temos um recorte ao dizer que o número é maior que 11. Se você parar para pensar, os possíveis números maiores que 11 são n(s) = {12,13,14,15,16,17,18,19,20}. Então temos 9 possibilidades dentre as quais temos que selecionar apenas os múltiplos de 4, o que resulta num conjunto de 3 elementos: A = {12, 16, 20}.
Logo, a probabilidade de ser um múltiplo de 4 no novo espaço amostral é de

Ou seja, para calcular a probabilidade de um evento, é necessário levar em consideração o espaço amostral. Quando você tem em mente como fazer o recorte desse espaço amostral, os cálculos serão facilitados para você.
Videoaula
Veja esse vídeo do Descomplica sobre probabilidade condicional e tire todas as suas dúvidas. Boa sorte nas provas!
Exercícios sobre probabilidade condicional
01 – (UEG GO/2019)
Dois candidatos, A e B, disputam a presidência de uma empresa. A probabilidade de o candidato A vencer é de 0,70; ao passo que a de B vencer é de 0,30. Se o candidato A vencer essa disputa, a probabilidade de Heloísa ser promovida a diretora dessa empresa é de 0,80; já se o candidato B vencer, essa probabilidade será de 0,30. A probabilidade de Heloísa, após a disputa da presidência dessa empresa, ser promovida a diretora, é de
a) 0,50
b) 0,45
c) 0,65
d) 0,56
e) 0,55
02 – (USF SP/2018)
Em um hospital com 160 funcionários, 60% são graduados e 70% são do sexo masculino. Sabe-se ainda que das pessoas de sexo feminino são graduados. A partir dessas informações, é correto afirmar que, escolhido ao acaso um desses funcionários, a probabilidade de ele ser do sexo masculino e graduado é
a) 1/3 .
b) 2/5.
c) 1/2.
d) 1/5.
e) 5/32 .
03 – (ESPM SP/2018)
Em um conjunto de números naturais há 23 números pares, 17 múltiplos de 3, 12 múltiplos de 6 e 7 números primos maiores que 3. Escolhendo-se ao acaso um desses números, a probabilidade de que ele seja múltiplo de 2 ou de 3 é:
a) 3/5.
b) 5/6
c) 4/5
d) 1/2
e) 3/4
Gabarito:
- C
- B
- C

