Diâmetro; Tangente; Secante; e Corda. Aprenda agora os segredos da circunferência e das relações métricas nela existentes. É básico no estudo e compreensão da matemática. Acompanhe esta aula e fique preparado para qualquer questão do Enem e dos vestibulares!
Desde a invenção da roda pelos antigos povos mesopotâmicos, muito se tem estudado sobre a circunferência. Esses povos descobriram que a roda deixava o transporte mais rápido e mais fácil. A partir disso, passaram a calcular inúmeras relações métricas na circunferência, entre uma circunferência e outra, e assim por diante.
Depois, aperfeiçoando ainda mais o método de transporte, criou-se a roldana para suspender objetos mais pesados, as engrenagens e os moinhos de água. Até mesmo se pode calcular e estimar questões da astronomia e que envolvem o mundo que nos cerca através da circunferência.
Alerta: Círculo é diferente de Circunferência
Muita gente se perde nas provas do Enem e dos vestibulares porque confunde Círculo com Circunferência. São duas coisas completamente diferentes. Confira as diferenças agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito:
Agora ficou mais claro pra você o que é um círculo, eo que é uma circunferência? Então, bora avançar para as Relações Métricas da Circunferência.
Elementos de uma circunferênciaAntes de iniciar a aula sobre relações métricas na circunferência, é importante lembrar alguns conceitos e o que eles significam, para que não haja dúvida na hora das explicações posteriores. Observe a imagem:
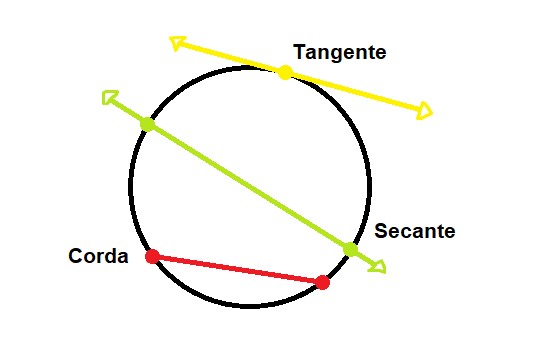
- Corda é qualquer segmento de reta cujos pontos das extremidades pertencem à circunferência.
- Diâmetro é a maior corda que uma circunferência possui.
- Tangente é qualquer reta que tem um único ponto em comum com a circunferência.
- Secante é qualquer reta que tem dois pontos em comum com a circunferência.
Relações métricas na circunferência
Agora que você já conhece algumas nomenclaturas importantes dos segmentos da circunferência, está na hora de conhecer as relações de semelhança que ocorrem entre circunferência, segmentos de retas e pontos. Vamos lá?
Cruzamento entre duas cordas
Quando duas cordas se cruzam no interior de uma circunferência, o ponto de cruzamento determina segmentos de reta que são proporcionais entre si. Essa proporcionalidade pode ser dada através de uma multiplicação. Veja o esquema:
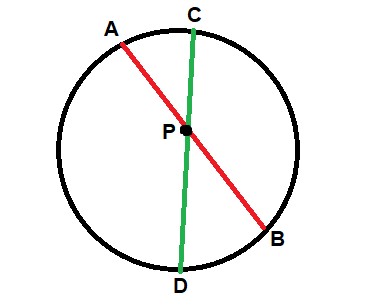
O segmento AP multiplicado pelo segmento PB é proporcional ao segmento CP multiplicado pelo segmento PD. Veja a representação a seguir para entender melhor:
AP * PB = CP * PD
Dica: Você conhece o Geogebra? É um programa bastante utilizado para demonstrações em geometria, acesse o link e veja os exemplos de relações métricas na circunferência, mova os pontos e veja o que acontece!
O Círculo Trigonométrico ajuda você
Confira com o professor Lucas Borguezan os macetes do Círculo Trigonométrico para você gabaritar nas relações métricas da circunferência:
Dois segmentos secantes saindo do mesmo ponto
Se você traçar dois segmentos secantes a uma circunferência que se interceptam em um ponto externo, você criará uma relação de semelhança entre a medida dos segmentos externos à circunferência e a medida do segmento inteiro. Isso ocorre independente do tamanho da circunferência. Observe:
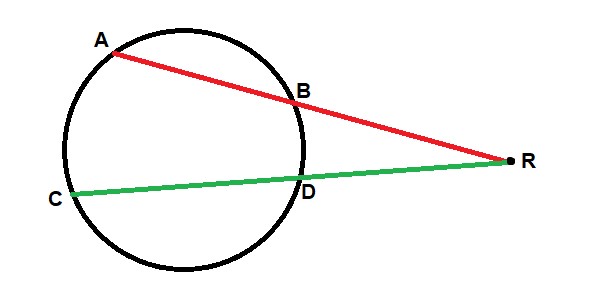
O segmento AR multiplicado pelo segmento BR é proporcional ao segmento CR multiplicado pelo segmento DR, assim:
AR * BR = CR * DR
Exemplo:
Na imagem abaixo, calcule o tamanho do segmento CD
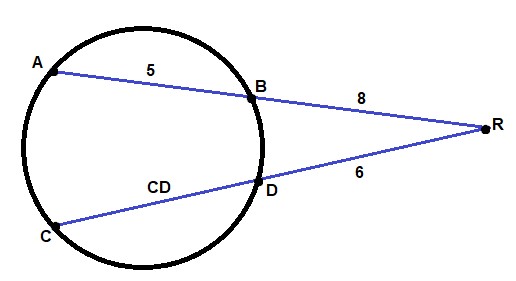
Solução: Tendo as unidades de comprimento de cada segmento, podemos utilizar a regra de proporcionalidade:
AR * BR = CR * DR
Assim:
(5 + 8) * 8 = (CD + 6) * 6
13 * 8 + (CD + 6 * 6
104 = 6 CD + 36
6 CD = 104 – 36
CD = 68/6
CD = 34/3 ou ainda 11,34 unidades de comprimento.
Enfim, parece que circunferência nos cerca desde sempre. Vamos descobrir um pouco mais?

Segmento secante e segmento tangente partindo de um mesmo ponto
Ao se traçar um segmento secante e um segmento tangente a uma circunferência, sendo que estes segmentos de reta se encontram em um ponto externo a circunferência, estes segmentos irão se relacionar da seguinte forma:
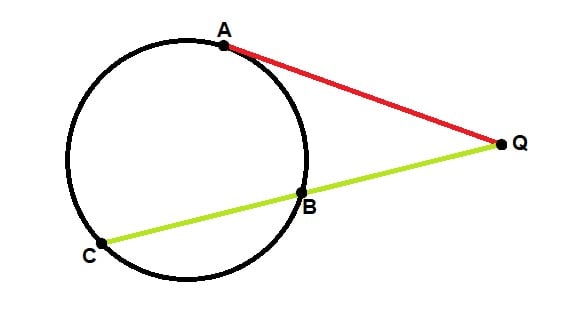
O quadrado da medida do segmento tangente é igual a multiplicação da medida do segmento secante pela medida de sua parte externa, sendo assim:
(AQ)² = CQ * BQ
Ordenada de um ponto e diâmetro
A ordenada de um ponto P da circunferência em relação a um diâmetro é a média geométrica entre os segmentos AM e BM determinados por este diâmetro.
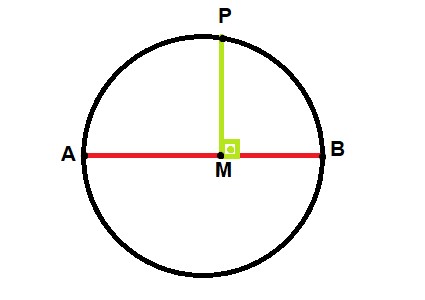
A relação entre as retas se dá por:
(PM)² = AM * BM
Diâmetro e projeção da corda
A corda PB traçada da extremidade de um diâmetro é a média geométrica entre o diâmetro AB e a projeção desta corda sobre ele BM.
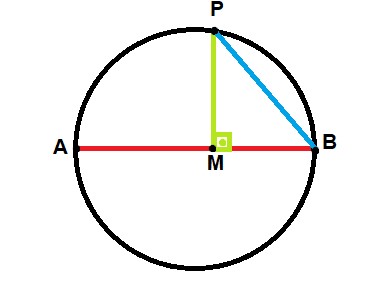
A relação entre essas retas se dá da seguinte maneira:
(PB)² = AB * BM
Para entender melhor, veja um exemplo:
Calcule o valor da corda PA na figura abaixo:
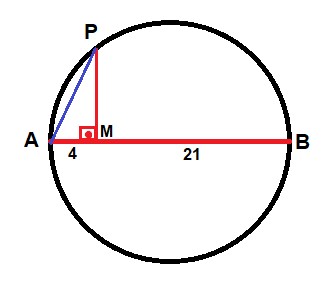
Solução: Para calcular o tamanho da corda, basta observar o tamanho dos segmentos AB e AM, assim, utilizando a correspondência:
(PA)² = AB * AM
PA² = (21 + 4) * 4
PA² = 25 * 4
PA = √100
PA = ±10
Por se tratar de uma unidade de comprimento, utilizamos somente o resultado positivo, já que uma unidade de medida negativa não configura uma distância.
Videoaula
Por fim, para complementar ainda mais seus conhecimentos, acesse a aula do canal Nerckie:
Exercícios
Para finalizar seus estudos sobre as relações métricas na circunferência, resolva os exercícios abaixo, selecionados pela professora Andréia!
Questão 01)
Observe a figura
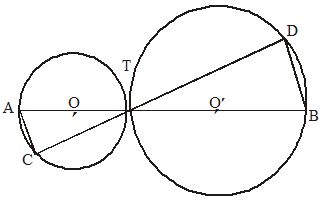
Nessa figura, contém os centros O e O’ das circunferências que se tangenciam no ponto T . Sendo AB = 44, O‘B = 16 e AC = 6, a medida TD é :
a) 8
b) 15
c) 6
d) 20
e) 16
Questão 02)
Na figura abaixo têm–se as circunstâncias de centros O1 e O2, tangentes entre si e tangentes à reta r nos pontos A e B, respectivamente.
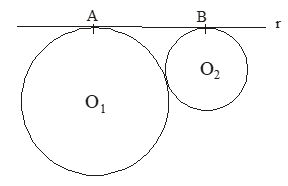
Se os raios das circunferências medem 18cm e 8cm, então o segmento mede, em centímetros:
a) 20
b) 22
c) 23
d) 24
e) 26
Questão 03)
Na circunferência de centro O, representada pela figura ao lado, o raio mede 4u.c., a distância de P a A mede 3u.c. e a reta PT é tangente à circunferência.
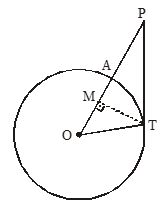
Nessas condições, é correto afirmar:

01) Gab: E
02) Gab: D
03) Gab: 14

