Já prestou atenção em quantas coisas do nosso dia a dia possuem simetria entre si? Tanto na natureza, quanto em construções, é muito comum perceber a simetria. Na matemática não é diferente! Vem comigo nesta aula para compreender a simetria entre figuras!
Você que passa bastante tempo na internet já deve ter ouvido falar no conceito de harmonização facial. Essa tendência do mundo da moda e estética divide opiniões. Mas qual o propósito? Bem, é um procedimento cirúrgico que busca deixar o rosto mais bonito através da simetria.
Geralmente o conceito de beleza está diretamente associado ao conceito de simetria. Muitos dos grandes artistas a utilizam em suas obras, e não somente isso, até mesmo na música.
Em grandes construções e na natureza é possível identificar padrões que seguem esse comportamento. Uma das maneiras de identificar ou criar padrões simétricos é através da matemática. Acompanhe essa aula e descubra como.
O que é simetria?
Matematicamente falando, a simetria é a preservação do formato da imagem e da sua configuração através de uma reta ou um ponto. Ao reproduzir uma imagem simetricamente estaremos preservando suas características primeiras, tais como os ângulos, a medida do lado, o tipo de imagem e, principalmente, seu tamanho.
Reconhecer um padrão simétrico intuitivamente é fácil, nosso cérebro está acostumado à repetição em mosaicos, telas e na natureza. Confira os tipos de simetria.
Tipos de simetria
No estudo da matemática, existem variados tipos de simetria, e elas diferem entre si. Essa ferramenta matemática é bastante utilizada em diversos segmentos, inclusive na computação gráfica. Hoje você vai aprender um pouco sobre a simetria por reflexão e por rotação.
Guarde bem os conceitos e exemplos para solucionar os exercícios! Comece agora com a Introdução aos tipos de Simetria com o professor Lucas Borguezan, do canal do curso Enem Gratuito:
Simetria por reflexão
A simetria por reflexão é, como o próprio nome indica, um reflexo, um espelhamento da imagem através de um eixo de simetria. Esse eixo de simetria pode ser uma reta ou até mesmo um ponto.
Além disso, é importante salientar que o ponto original de uma imagem e seu correspondente na reflexão têm a mesma distância em relação ao eixo de simetria.
Exemplo de simetria por reflexão
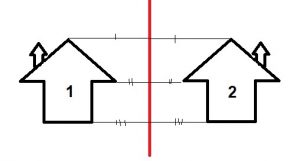
Na imagem, o segmento de reta em vermelho é o eixo de simetria, a casinha 1 é a imagem original e a casinha 2 é sua correspondente na reflexão. Perceba como os pontos que compõem a figura 1 e os pontos que compõem a figura 2 possuem a mesma distância do eixo de simetria. Isso significa que entre elas existe uma simetria.
Todo esse papo de eixo e pontos não lembrou alguma coisa pra você? Esses termos são bastante utilizados lá no estudo do plano cartesiano. O conceito de simetria é bastante utilizado também no estudo de gráficos e funções. Veja um exemplo:
Exercício resolvido
Qual é o ponto que corresponde ao simétrico do ponto P(3,2) em relação ao eixo y?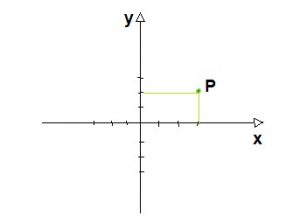
Solução: perceba que o exemplo traz o eixo dos y como sendo o eixo de simetria. Logo, a distância entre o ponto correspondente e o eixo y precisa ser igual à distância entre o ponto P e o eixo y. Essa distância é 3 unidades, veja: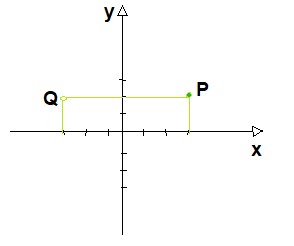
Logo, o simétrico do ponto P(3,2), em relação ao eixo dos y é o ponto Q (-3,2).
Além de ocorrer através de um eixo de simetria, a reflexão também pode ser dada através de um ponto de simetria. Mas, nesse caso, é preciso prestar atenção, pois a imagem correspondente não será somente a imagem espelhada, ela também estará invertida.
Veja outro exemplo. Observe a simetria por reflexão através de um ponto da letra F:
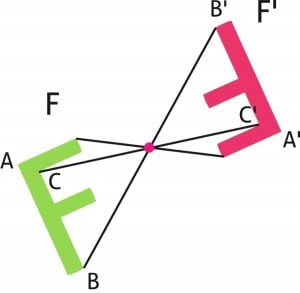
Perceba que ao criar um correspondente simétrico através de um ponto a imagem fica invertida, diferentemente da reflexão através de uma reta. Esse é um caso especial também de simetria por rotação que você verá a seguir.
Simetria por rotação
Para criar um correspondente simétrico através da rotação, basta apenas “girar” a imagem original ao redor de um ponto que chamaremos de centro de rotação. A distância entre a imagem e o centro de rotação se mantém constante, e a medida que a imagem gira chamaremos de ângulo de rotação.
Exemplo de simetria por rotação
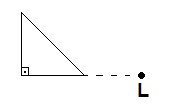
Girar a figura 90º no sentido horário, em relação ao ponto L.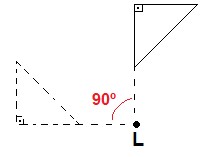
Para girar uma imagem e encontrar seu simétrico através de rotação, devemos prestar atenção ao ângulo da rotação e ao sentido da rotação, que será horário ou anti-horário.
Existe uma rotação específica na simetria por rotação em que o correspondente simétrico é exatamente o mesmo do que se tivéssemos feito simetria por reflexão.
Isso se dá quando utilizamos o ângulo de rotação de 180º, independente do sentido. Veja no exemplo através da imagem: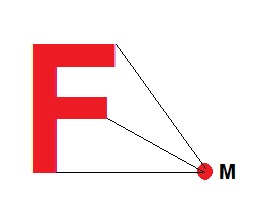
Outro exemplo: gire a figura 180º no sentido horário, em relação ao ponto M.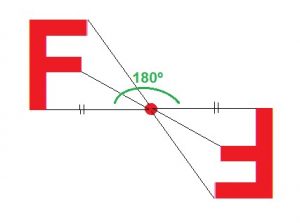
Veja como todos os pontos da letra F e seus correspondentes fizeram o giro de 180º, mas também mantiveram a mesma distância em relação ao ponto M. Logo, ocorre simetria por reflexão e por rotação ao mesmo tempo.
Continue estudando para as provas do vestibular e Enem e perceba a relação entre essa aula e aula de física óptica.
Exercícios sobre simetria
Agora, resolva os exercícios abaixo selecionados pela professora e verifique se você realmente aprendeu o conteúdo desta aula. Se você tiver dúvidas ou errar algum exercício, faça uma revisão e volte para refazer a questão.
Questão 01)
Um programa de edição de imagens possibilita transformar figuras em outras mais complexas. Deseja-se construir uma nova figura a partir da original. A nova figura deve apresentar simetria em relação ao ponto O.
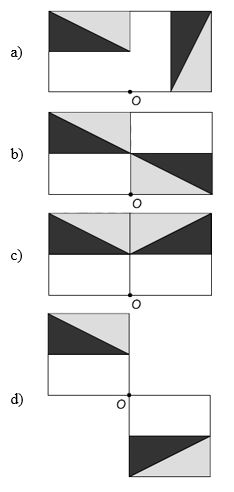
A imagem que representa a nova figura é:
Questão 02)
Simetrias são encontradas, frequentemente, em nosso dia-a-dia. Elas estão nas asas de uma borboleta, nas pétalas de uma flor ou em uma concha do mar. Em linguagem informal, uma figura no plano é simétrica quando for possível dobrá-la em duas partes, de modo que essas partes coincidam completamente.
De acordo com a descrição acima, qual das figuras a seguir é simétrica?
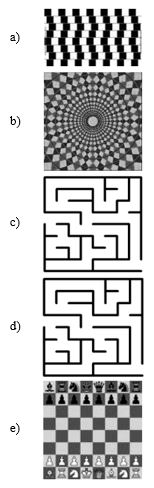
1) Gab: E
2) Gab: B
