7 temas de Matemática que mais caem no Enem
Descubra como a Matemática do Enem aparece no dia a dia e aprenda os 7 tópicos que mais caem, com foco na aplicação e na interpretação.
A prova de Matemática e suas Tecnologias é uma das mais decisivas do Enem. O segredo é entender que a prova não é cobrada de forma solta ou puramente teórica. Ela aparece como uma ferramenta pra resolver situações reais do dia a dia: gastos, crescimento de uma doença, medição de terrenos… coisas que fazem parte da nossa rotina.
Por isso, a melhor estratégia é dominar os sete tópicos que mais aparecem, sempre com foco na aplicação prática e no contexto. E não esquece: antes mesmo de começar a fazer as contas, interpretar bem o texto é o passo número um pra descobrir qual ferramenta usar! Bora entender?
Razão e Proporção
Razão e Proporção são o ponto de partida de TUDO na Matemática aplicada. Eles nos mostram a relação entre diferentes grandezas e como elas variam.
- Razão: é uma comparação entre duas coisas, geralmente feita por meio de uma divisão. Exemplo: se você tem 30 anos e seu amigo tem 10, a razão entre as idades é 30/10 (ou 3/1). Simples assim. Matematicamente: A/B ou A:B.
- Proporção: é a igualdade entre duas razões (A/B = C/D). É o que garante que uma relação de mudança se mantém.
Aplicações e a Regra de Três
A aplicação mais direta da proporção é a famosa Regra de Três, que resolve a maioria dos problemas de variação. É crucial saber classificar a relação:
- Diretamente Proporcional: se um aumenta, o outro aumenta na mesma medida (Ex: Se eu trabalho mais horas, recebo um salário maior).
- Inversamente Proporcional: se um aumenta, o outro diminui (Ex: Se eu aumento a velocidade, o tempo de viagem diminui).
Conexão com a Função Afim
Dominar esse assunto é o que te prepara para a Função Afim (1º grau). Por quê? Porque essa relação te ensina a calcular a taxa de mudança entre as coisas. Essa taxa (o coeficiente angular) é o conceito central da Função Afim.
Se você tem dificuldade na Regra de Três, provavelmente terá dificuldade na interpretação do coeficiente.
Função Afim (1º grau)
As Funções Afins (ou de 1º grau) são as funções das retas inclinadas e que aparecem muito em Física (como no estudo dos Movimentos Retilíneos e seus gráficos) assim como na análise de gráficos de Química, Biologia e Tratamento da Informação.
Fórmula e gráfico
A cara dela é f(x) = ax + b. O gráfico é sempre uma linha reta.
Interpretação dos coeficientes
Toda a análise da função depende de entender o que cada letra significa:
- a (Coeficiente Angular): é a taxa de variação ou a inclinação da reta.
- Se a > 0, a função cresce. Se a < 0, a função decresce.
- No mundo real: é o valor variável (Ex: Custo por quilômetro rodado).
- b (Coeficiente Linear): é o valor fixo ou inicial. É onde a reta “corta” o eixo y (o valor de f(x) quando x=0).
- No mundo real: é a taxa inicial (Ex: A bandeirada fixa do táxi ou uma mensalidade).
Como o Enem cobra
Aparece muito em problemas de tarifas e custos. O exemplo clássico é a corrida de táxi: uma taxa fixa (b) somada a um valor variável (a) por km rodado.
A parte mais avançada é a comparação de duas ou mais funções lineares (duas retas em um gráfico). Você precisa saber que a reta mais inclinada (maior valor de a) indica o crescimento ou decaimento mais rápido.
Função Quadrática (2º grau)
A Função Quadrática (ou de 2º grau) é uma função R → R, ou seja, uma função em que o domínio e o contradomínio são iguais ao conjunto dos números reais.
Fórmula e gráfico
A cara dela é f(x) = ax2 + bx + c. O gráfico é uma parábola.
- Se a > 0, a boca da parábola é para cima (ponto de mínimo).
- Se a < 0, a boca da parábola é para baixo (ponto de máximo).
O Vértice
O ponto mais importante da parábola é o Vértice (V), pois ele marca o valor extremo (máximo ou mínimo) que a função pode atingir. Suas coordenadas são:
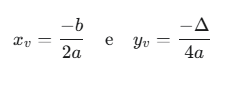
Como cai no Enem
O Enem ama usar a Função Quadrática em problemas de otimização. Se você ler as palavras-chave “máximo” ou “mínimo“, já sabe: é hora de calcular o Vértice. Exemplos: maximizar lucros, minimizar custos ou encontrar a altura máxima de um lançamento.
É vital não confundir xv e yv:
- O xv (eixo horizontal) responde: “Para qual valor…?” (Ex: Qual preço, qual quantidade, em qual tempo?).
- O yv (eixo vertical) responde: “Qual é o valor…?” (Ex: Qual é o lucro máximo, qual é a altura máxima?).
A confusão entre o que está sendo maximizado (o valor y) e quando isso acontece (o valor x) é um erro comum, e o foco deve ser sempre na interpretação da coordenada correta do Vértice.
Função Exponencial
A Função Exponencial é a modelagem do crescimento ou decaimento ACELERADO, onde a taxa de variação não é constante, mas sim proporcional à quantidade que já existe.
Fórmula e características
A chave é f(x) = a . bx. O gráfico é uma curva acentuada que nunca toca o eixo x.
- a (Valor Inicial): é a quantidade no ponto de partida.
- b (Fator Multiplicativo): Define o comportamento. Se b > 1, há crescimento exponencial (multiplicação sucessiva); se 0 < b < 1, há decaimento.
Conexão interdisciplinar
A função exponencial é tipicamente cobrada em contextos interdisciplinares, com forte ligação com Biologia, Economia e Química.
- Finanças: clássicos problemas de Juros Compostos.
- Biologia: modelos de crescimento populacional ou cultura de bactérias, onde a colônia dobra em intervalos de tempo fixos.
- Decaimento: decaimento radioativo (Química) ou depreciação acelerada de bens.
Para resolver, você precisa saber manipular equações para que ambos os lados tenham a mesma base, o que permite comparar os expoentes.
Geometria Plana
Geometria Plana no Enem é focada, na maioria das vezes, no cálculo de Áreas e Perímetros de figuras que representam objetos ou espaços reais (terrenos, pisos, etc.).
Figuras e fórmulas que você PRECISA saber
É o básico do básico, mas a dificuldade está na aplicação em problemas complexos:
- Quadrado: A = l²
- Retângulo/Paralelogramo: A = b . h
- Triângulo: A = (b . h) / 2
- Trapézio: A = ((B + b) . h) / 2
- Círculo: Área A = π . r² e Circunferência C = 2 . π . r
Além das áreas, o Teorema de Pitágoras e a Semelhança de Triângulos são ferramentas indispensáveis para achar medidas que faltam.
A visualização como ferramenta de resolução
As questões raramente dão a figura pronta. O examinador descreve um terreno, um galpão ou um objeto, e espera que você desenhe e decomponha a figura complexa em formas mais simples (como retângulos e triângulos) para aplicar as fórmulas. Sua capacidade de visualização espacial e de interpretar plantas é tão importante quanto a memória das fórmulas.
Geometria Espacial
Geometria Espacial (3D) é a extensão da Plana, focando no cálculo de Volume e Área Total de sólidos. É fundamental em questões de logística, capacidade de reservatórios e uso de embalagens.
Conceito Base
Para prismas e cilindros, o volume é calculado multiplicando-se a Área da Base (Abase) pela Altura (h). Ou seja, V = Abase . h.
Para sólidos que afunilam (pirâmides e cones), o volume é um terço do volume do sólido correspondente: V = (Abase . h) / 3.
Fórmulas de Volume mais cobradas
O foco deve estar nos sólidos que representam armazenamento ou embalagens:
- Cubo: V = a³.
- Paralelepípedo (ou Bloco Retangular): V = c . l . h
- Cilindro: V = π . r² . h
- Esfera: V = (4/3) . π . r³
O desafio da conversão de unidades
Este é o ponto que eleva a dificuldade: a conversão entre o volume matemático e a capacidade real. É obrigatório saber:
- 1 m3 = 1000 Litros
- 1 dm3 = 1 Litro
As questões frequentemente envolvem a relação entre volume e capacidade (Ex: Quantos litros cabem no reservatório?) ou a conservação de volume (Ex: Quantos cubos menores podem ser feitos se eu derreter um cone?).
Estatística
Estatística e Probabilidade, junto com a análise de gráficos, são consistentemente os temas de maior incidência na prova. A maior parte das questões exige que você organize e interprete dados apresentados em tabelas e gráficos.
Medidas de Tendência Central (MTC)
O foco principal são as três Medidas de Tendência Central (MTC): Média, Moda e Mediana. Você precisa saber calcular e, principalmente, interpretar cada uma:
- Média Aritmética: é o valor de equilíbrio. Calcula-se somando tudo e dividindo pela quantidade de itens. Atenção: O Enem adora usar a Média Ponderada, onde cada valor tem um “peso” diferente (Ex: notas com pesos distintos).
- Moda: é o valor que mais se repete. Em um gráfico, é a barra ou o setor mais alto.
- Mediana: é o valor central do conjunto. Para achá-la, você PRECISA ordenar os dados (crescente ou decrescente).
- Se o número de dados é ímpar: é o termo do meio.
- Se for par: é a média dos dois termos do meio.
Por que a mediana é importante?
A Média é muito sensível a outliers (valores discrepantes, muito altos ou muito baixos), que podem distorcer o valor central. A Mediana, por depender só da posição, não é afetada por esses extremos.
No Enem, isso se traduz em perguntas sobre qual medida representa melhor um conjunto de dados, especialmente em contextos como análise de salários. Nesses casos, a Mediana é geralmente a medida mais estável e representativa da realidade.
Quer saber mais? Vem aí o Aulão Enem 2025!
Curtiu esse conteúdo? Então se prepara, porque isso aqui é só um gostinho do que vem por aí!
Esse material é só uma prévia do nosso aulão de Matemática, que faz parte do Aulão Enem 2025! Lá no canal do Curso Enem Gratuito, você vai poder acompanhar duas semanas de lives gratuitas, com professores incríveis revisando os temas que mais caem em todas as áreas do Enem.
🗓️ Anota na agenda: no dia 12 de novembro, às 19h, tem aulão de Matemática com o queridíssimo professor Marcus, direto no YouTube do Curso Enem Gratuito.
Sobre o(a) autor(a):
Luana Santos - Formada em Jornalismo pela Universidade Federal de Santa Catarina, é redatora com foco em educação, produção de conteúdo para o Enem e vestibulares. Atualmente, integra a equipe da Rede Enem, onde cria materiais informativos e inspiradores para ajudar estudantes a alcançarem seus objetivos acadêmicos. Ama café, livros e uma boa conversa sobre educação.
