O que é velocidade relativa? Onde a encontramos? O que é a lei dos cossenos e para quê serve? O que é composição de movimentos? Revise isso e muito mais nesta aula de Física para o Enem e vestibulares!
Nessa aula, você vai aprender tudo sobre velocidade relativa e vai ver que ela está muito presente em nosso dia a dia. Também irá aprender sobre a lei dos cossenos e como utilizá-la para compreender composição de movimentos, um tema sempre presente nos vestibulares.
Você já deve saber que a velocidade de um corpo é dada pela relação entre o seu deslocamento e o intervalo de tempo em que este deslocamento acontece, certo? Então, nesta aula você vai aprender sobre um tipo diferente de velocidade: a velocidade relativa.
Analisaremos a velocidade de móvel, agora em relação a um outro móvel. No seu cálculo poderemos utilizar todas as fórmulas e funções utilizadas no estudo do M.R.U. e M.R.U.V.
Para calcular a velocidade relativa temos necessariamente que levar em conta, além do valor da velocidade, sua direção e sentido. Sendo assim, a trataremos como velocidade vetorial.
O que é velocidade relativa?
O conceito de velocidade relativa está muito presente em nosso dia a dia. Como você viu acima, a velocidade relativa é utilizada quando comparamos a velocidade de um móvel em relação a outro móvel.
Por exemplo, em uma rodovia quando trafegamos com carros no mesmo sentido ou sentido oposto, quando corremos a favor ou contra o vento, quando subimos ou descemos em uma escala rolante, etc.
Sendo assim, temos dois tipos de velocidades relativa: uma de Aproximação e outra de Afastamento.
Velocidade Relativa de Aproximação
Essa velocidade é observada quando dois móveis quaisquer estão se movimentando em sentidos opostos, ou no mesmo sentido e um vier a ultrapassar o outro. No caso de estiverem em sentidos opostos, a velocidade de um em relação ao outro será a soma das duas velocidades. E, quando estiverem no mesmo sentido devemos subtrair a velocidade um do outro. Vejamos um exemplo de cada:
- Um carro A se movimenta em certa rodovia com velocidade constante de 100 km/h indo de encontro a um outro carro B em outra pista, que também se movimenta com velocidade constante de 80 km/h. De acordo com a orientação abaixo:
Para o carro A, no momento em que B passa ao lado, a velocidade de B é 180 km/h. Da mesma forma, para B, a velocidade do carro A, no momento que passa ao lado, será 180 km/h.
- Nessa outra situação, vemos que o carro A irá ultrapassar o carro B pois está 20km/h mais rápido. A partir disso, podemos observar ainda que a cada hora, o carro A está 20 km mais próximo de B. Então, no momento da ultrapassagem para o carro B, a velocidade do carro A será 20 km/h.
Portanto, percebemos que a velocidade relativa envolve mais um conceito importante, que trata da direção e sentido da trajetória dos corpos. Portanto, você precisa ficar atento(a) à estas informações para não ter problemas na resolução dos exercícios!
Velocidade Relativa de Afastamento
Essa velocidade de afastamento tem seu cálculo igual à de aproximação. Isso porque ela surge após o momento do encontro dos veículos.
Quando os dois veículos estão no mesmo sentido, momentos após o que está atrás ultrapassar o veículo da frente, ocorrerá o afastamento, e quando estiverem em sentidos opostos, após o encontro, eles se afastarão um do outro. O cálculo é o mesmo da velocidade relativa de aproximação.
Resumindo:
Sentidos opostos -> velocidades somadas
Sentidos iguais -> velocidades subtraídas
Lei dos cossenos
A lei dos cossenos é uma de forma de calcular um ângulo ou um lado desconhecido de um triângulo qualquer, uma vez que conhecemos as outras medidas. É uma extensão do teorema de Pitágoras que somente funciona para triângulo retângulo. A lei dos cossenos diz:
“Em qualquer triângulo, o quadrado de um dos lados corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.”
Matematicamente falando temos:
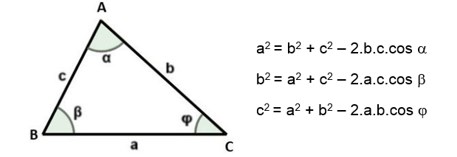
Observe que quando o ângulo for 90o, o termo 2.a.b.cos do ângulo some, pois cosseno de noventa é zero. Isso é totalmente entendido, uma vez que o ângulo sendo noventa, a figura será um triângulo retângulo, valendo o teorema de Pitágoras!
Saiba mais nessa aula do professor Lucas, no nosso canal do Youtube:
Aplicando a Lei dos Cossenos em Física
Imagine que você tem dois vetores que podem representar qualquer grandeza, (velocidade, força, impulso, etc), unidos em sua extremidade por um ângulo e deseje saber qual a soma deles. Nessa situação fazemos uso da lei dos cossenos para resultante, isto é:
Sendo a e b os dois vetores somados, q o ângulo entre eles e c, a soma dos vetores a e b. Observe que o segundo sinal é de +, pois agora estamos somando.
Considere o vetor 
de medida 8cm e o vetor 
de medida 6cm. Estão ligados pela extremidade por um ângulo de 30o, conforme figura. Determine a soma deles.
Aplicando a lei dos cossenos para soma de vetores, temos:
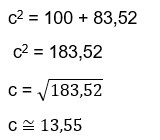
Portanto a soma dos vetores a e b tem medida de 13,55cm.
Agora que você entendeu como utilizamos a lei dos cossenos, passaremos agora para um novo tópico.
Composição de movimentos
Vamos compreender composição de movimentos em três exemplos:
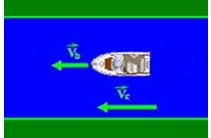
1º Considere um barco navegando a favor da correnteza de um rio conforme figura. No barco está marcando 45 km/h e admita que a velocidade da correnteza é de 10 km/h. Qual seria a velocidade do barco para uma pessoa que está as margens do rio?
Como estão na mesma direção e mesmo sentido, somamos. Portanto, para a pessoa na margem o barco se deslocará com velocidade 55 km/h.
2º Considere agora, ele navegando contra a correnteza do rio conforme figura. O barco continua navegando com 45 km/h e a velocidade da correnteza continua a mesma, 10 km/h. Qual seria a velocidade do barco para uma pessoa que está as margens do rio?
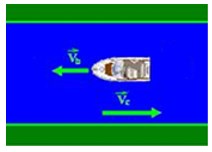
Observe que as duas velocidades têm sentidos opostos, então, para a pessoa na margem o barco estará indo mais devagar do que os 45 km/h. Temos então que subtrair a velocidade da correnteza. Portanto, para a pessoa presente na margem, o barco de desloca com velocidade de 35 km/h. Entendeu? Fácil né?
Vamos agora ao terceiro exemplo:
3º Agora considere que o barco está saindo da margem do rio no sentido de atravessá-lo perpendicularmente. Vamos manter os mesmos valores para as velocidades do barco e da correnteza. Observe o desenho e determine com qual velocidade o barco estará de fato cruzando o rio.
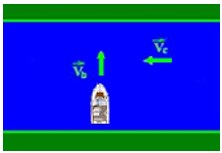
Observe que o sentido das velocidades faz um ângulo de 90o, pois são perpendiculares. Portanto, para soma delas, teremos que utilizar o teorema de Pitágoras. Lembra dele?
“O quadrado da hipotenusa é igual a soma do quadrado dos catetos”
Representando por vetores, temos:
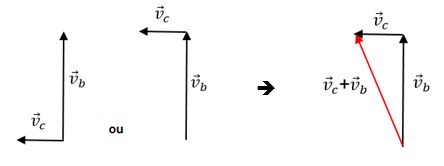
Resolvendo…
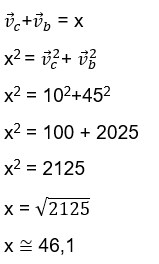
Portanto, a velocidade do barco observada pela pessoa na margem será aproximadamente 46,1 km/h.
Aí você pergunta: E se for outro ângulo, como faço? E eu respondo: Você usa a lei dos cossenos para resultante!
Você pode aprender um pouco mais sobre composição de movimentos assistindo ao vídeo abaixo
Agora, que tal testar o que você aprendeu resolvendo exercícios sobre velocidade relativa?
Questão 01 – (UEMG/2015)
O tempo é um rio que corre. O tempo não é um relógio. Ele é muito mais do que isso. O tempo passa, quer se tenha um relógio ou não.
Uma pessoa quer atravessar um rio num local onde a distância entre as margens é de 50 m. Para isso, ela orienta o seu barco perpendicularmente às margens.
Considere que a velocidade do barco em relação às águas seja de 2,0 m/s e que a correnteza tenha uma velocidade de 4,0 m/s.
Sobre a travessia desse barco, assinale a afirmação CORRETA:
a) Se a correnteza não existisse, o barco levaria 25 s para atravessar o rio. Com a correnteza, o barco levaria mais do que 25 s na travessia.
b) Como a velocidade do barco é perpendicular às margens, a correnteza não afeta o tempo de travessia.
c) O tempo de travessia, em nenhuma situação, seria afetado pela correnteza.
d) Com a correnteza, o tempo de travessia do barco seria menor que 25 s, pois a correnteza aumenta vetorialmente a velocidade do barco.
Gab: B
Questão 02 – (UEPG PR/2015)
Um barco movimenta-se com velocidade igual a 10m/s em relação à água. A correnteza se movimenta em relação às margens com velocidade de 2m/s. A respeito desses movimentos, assinale o que for correto.
01. Se o barco tem seu leme dirigido rio abaixo, sua velocidade em relação às margens é de 12 m/s.
02. Se o barco deve atingir um ponto na margem oposta, exatamente à frente do ponto de partida, a velocidade resultante em relação às margens deve ser menor que 9 m/s.
04. Se o barco mantém seu leme numa direção perpendicular à margem, a velocidade resultante em relação às margens é maior que 10 m/s.
08. Se o barco tem seu leme dirigido rio acima, sua velocidade em relação às margens é de 8 m/s.
16. Se em certo trecho, a correnteza aumentar sua velocidade para um valor maior que 10 m/s, o barco, com seu leme dirigido para cima, não conseguirá subir o rio.
Gab: 29
Questão 03 – (USF SP/2016)
Um menino de massa 40 kg está parado em pé na extremidade de uma canoa de massa 200 kg, que também se encontra parada sobre uma lagoa de águas calmas. Desprezando o atrito entre a canoa e a água, se o menino andar 1 m em direção à extremidade oposta da canoa, verifica-se que a canoa nesse intervalo de tempo
a) fica parada na mesma posição.
b) desloca-se 1 m na mesma direção e sentido que o menino se deslocou na canoa.
c) desloca-se 1 m na mesma direção e sentido oposto ao que o menino se deslocou na canoa.
d) desloca-se 20 cm na mesma direção e sentido que o menino se deslocou na canoa.
e) desloca-se 20 cm na mesma direção e sentido oposto ao que o menino se deslocou na canoa.
Gab: E
