Operações com raízes sempre assustam quem está fazendo a prova. Mas não se preocupe! Ao final dessa aula de Matemática você estará craque em resolver equações irracionais!
Quando falamos em equações irracionais, estamos nos referindo a equações onde a variável se encontra dentro de um radical. Na verdade, quando se trata de conjuntos numéricos, a relação entre números irracionais e radiciação é bem perceptível. Nessa aula, vamos ver alguns tipos de equações irracionais e a maneira pela qual iremos solucionar cada uma delas. Mas fique tranquilo(a), a parte boa de estudar matemática é poder relacionar todos os conteúdos novos com os quais você já sabe. Vamos lá?
Equações irracionais são equações em que a variável se encontra interna ao radical. Ou seja, o “x” que geralmente procuramos buscar, está dentro da raiz. Quando essas equações aparecem para o(a) estudante, seja na hora da explicação ou até mesmo na hora da prova, surge uma certa preocupação por “não saber o que fazer”. Mas, uma coisa é certa: você precisa ter em mente algumas propriedades da radiciação e da potenciação para tirar de letra o estudo das equações irracionais.
Resolvendo equações irracionais
Um passo importante para iniciar a resolução de uma equação irracional é procurar transformá-la em uma equação racional. Vamos ver como isso ocorre através de um exemplo:
Exemplo 1:
Para tentar transformar essa equação irracional em uma equação racional, elevamos os dois lados da igualdade ao quadrado. Assim:
De acordo com as propriedades de radiciação, uma raiz elevada ao quadrado é eliminada. Logo, ficamos com:
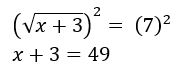
Aí é só resolver a equação resultante normalmente, isolando a variável. Veja:
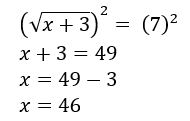
Antes de tomar o resultado obtido como verdadeiro, é preciso checar se a raiz pode ou não ser aceita como uma raiz da equação irracional dada. Para fazer essa verificação, basta substituir o resultado na equação inicial para verificar a igualdade.
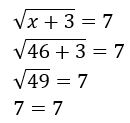
Agora sim, podemos garantir que x = 46 é solução da equação .
Este foi um exemplo bastante simples, onde tanto a variável x quanto o radicando apareceram somente uma vez. Agora, vamos ver um exemplo no qual temos duas raízes.
Exemplo 2: 
Nesse caso, a ideia inicial de elevarmos os dois lados da igualdade ao quadrado prevalece, porém, devemos prestar bastante atenção nas regras de fatoração. Veja:
Perceba que a parte 
é uma parte da fatoração que chamamos de quadrado da diferença e a ele se aplica a respectiva regra de fatoração. Logo:
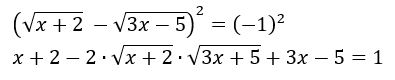
Desenvolvendo matematicamente, temos:
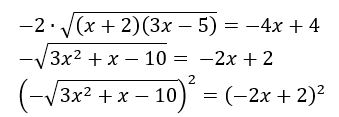
Preste atenção nesta parte. Você notou que precisamos elevar ao quadrado os dois lados da equação novamente? Isso não é um problema, durante a resolução de um exercício você pode se utilizar dessas estratégias quantas vezes forem necessárias. Desde que sejam feitas de forma prudente e respeitando as regras da matemática. Seguindo com o cálculo:
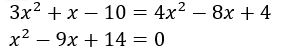
Perceba que obtivemos uma equação de segundo grau. Então, encontrando as raízes, temos:
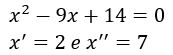
Assim como no exemplo anterior, você precisa agora fazer a verificação, para ver qual das raízes é válida. Substituindo as raízes x’ = 2 e x’’ = 7 na equação inicial:
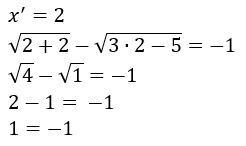
A raiz x = 2 não é válida.
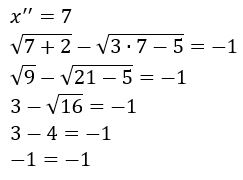
Como a igualdade confere, a raiz x = 7 é válida, logo a solução é x = 7.
Importante: para a solução das equações irracionais você só precisa se utilizar de dois passos básicos. O primeiro é elevar os dois lados de sua equação ao expoente equivalente a raiz e o segundo passo é fazer a verificação, para ter certeza que o resultado encontrado satisfaz a equação.
Gostou dessa aula? Percebeu como muitos conteúdos como potenciação, solução de equações de segundo grau e fatoração se fizeram presentes dentro de um conteúdo novo? Fique ligado, na matemática isso sempre acontece!
Quer mais conteúdo sobre equações irracionais? Então veja essa aula do professor Ferreto!
Exercícios:
Questão 01) A equação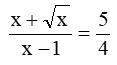 
em que x é um número real apresenta:
a) uma única raiz, que é maior que 10.
b) uma única raiz, que é menor que 10.
c) duas raízes cuja soma é 26.
d) duas raízes, mas só uma é maior que 10.
e) duas raízes, que são quadrados perfeitos.
Gab: A
Questão 02) O conjunto das soluções da equação 
é formado por
a) uma única raiz, a qual é um número real.
b) duas raízes reais.
c) duas raízes complexas.
d) uma raiz real e duas complexas.
Gab: A
