Equações Racionais: veja os macetes e como resolver
Encontrar o “x” da questão é o que vale ponto pra você na hora de resolver Equações. Aprenda de uma vez por todas para gabaritar na matemática do Enem e dos vestibulares.
Nesta aula você vai aprender a resolver exercícios de uma parte bem interessante da matemática, que também envolve frações. Estamos falando das equações racionais, também chamadas de equações fracionárias.
O que são equações racionais
O que determina que uma equação seja racional (ou fracionária) é que, pelo menos em um dos termos, apareça uma incógnita no denominador. A esse termo, damos o nome de fração algébrica.
Assim como fazemos em equações algébricas normais, para determinar o resultado da equação racional vamos nos valer de estratégias válidas na matemática, até que a variável tenha sido isolada em um dos lados da igualdade.
Veja, na prática, como resolver equações racionais
Aprenda agora com o professor de matemática Lucas Borguezan, do canal do Canal do Curso Enem Gratuito, como acertar na resolução das questões de Equações Racionais ou de Equações Fracionárias.
A maneira como você determina quais estratégias vai utilizar depende unicamente de você e da sua experiência enquanto estudante. Uns preferem utilizar a multiplicação cruzada, já outros escolhem calcular o mínimo múltiplo comum.
O que é uma Equação Definida
Dizemos que uma equação racional está definida quando em sua solução apresentam-se valores que pertencem ao conjunto dos números reais. O que isso significa? Isso significa que em uma fração o denominador jamais pode ser igual a zero (ou nulo).
Por isso, ao apresentar o conjunto solução devemos apresentar também as restrições. Mais adiante, nos exemplos, você vai entender melhor o que isso significa.
Lembra do Mínimo Múltiplo Comum?
Assim como no estudo das frações, para solucionar equações racionais uma ferramenta fundamental é o uso do mínimo múltiplo comum.
Resumo de Mínimo Múltiplo Comum
Confira com o professor Lucas Borguezan as dicas para você encontrar o Mínimo Múltiplo Comum. É para aprender e nunca mais esquecer:
Vamos ver em um exemplo como isso ocorre: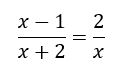
Perceba que os denominadores são x+2 e x.
O primeiro passo é verificar para quais valores esta equação está definida. Lembre-se que para ela estar definida, os denominadores precisam necessariamente ser diferentes de zero, então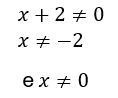
Isso significa que se alguma raiz for -2 ou 0 será eliminada pois não pertence à solução.
No segundo passo, para definir o mínimo múltiplo comum entre os denominadores, não é necessário fazer nenhum cálculo mirabolante. Basta multiplicar os dois denominadores. Sendo assim, temos: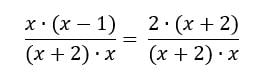
Como os dois denominadores são iguais, podemos desconsiderar, e continuar trabalhando com o restante.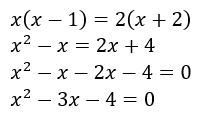
Resultamos então em uma equação do segundo grau, e as raízes podem ser determinadas via fórmula de Bhaskara. Para não perder o foco do estudo, vou apresentar as raízes e em seguida você confere se está tudo certo!
As raízes da equação acima são x’ = 4 e x” = -1. Nenhuma delas é igual a -2 ou a 0, então, o conjunto solução da equação é: 
Multiplicação cruzada de equações racionais
Para equações racionais simples como a do exemplo anterior, para simplificar os cálculos podemos fazer uma multiplicação cruzada, ao invés de calcular o mínimo múltiplo comum. Assim temos: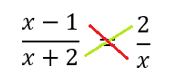
Fazendo a multiplicação cruzada, obtemos: x (x-1) = 2 (x+2)
Isso “encurta o caminho”. A partir disso calculamos normalmente, mas essa estratégia tem que ser usada com prudência.
Vamos ver outro exemplo: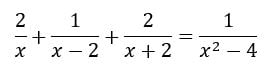
O primeiro passo é verificar para quais valores de x a equação não está definida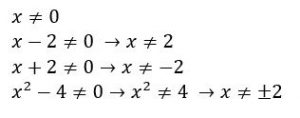
Segundo passo, calcular o MMC.
Importante: Ao calcular o MMC o conhecimento sobre fatoração se faz importante, já que 
equivale a 
.
Sendo assim, iremos fatorar o denominador por conveniência.
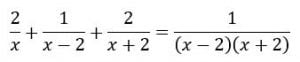
Fazendo os cálculos: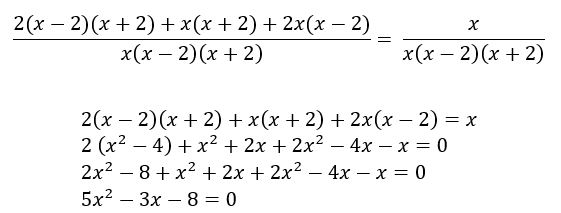
Usando Bhaskara para resolver a equação do segundo grau, obtivemos as raízes com resultados: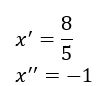
Como nenhum desses resultados é conflitante com os valores que tornam a equação indefinida, os dois são válidos. Logo o conjunto solução é dado por: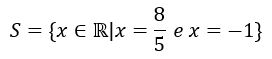
Videoaulas de apoio
Quer continuar estudando sobre equações racionais? Aqui tem uma sugestão de videoaula da Khan Academy!
Como resolver equações de segundo grau
Precisando relembrar como encontrar as raízes das equações de segundo grau? Veja com o professor Sérgio Sarkis, doVer Post canal do Curso Enem Graruito. Vem, que ele te ajuda!
Exercícios sobre equações racionais
Para terminar, resolva os exercícios sobre equações racionais a seguir e verifique se você compreendeu o conteúdo dessa aula.
Questão 01) A soma das raízes da equação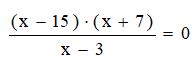 
é:
a) 9
b) 11
c) 10
d) 8
e) 12
Gab: D
Questão 02) A soma das raízes da equação é igual a:
a) 1
b) 4
c) –3
d) 0
e) –1
Gab: E
Sobre o(a) autor(a):
Andréia Zanchetti - Os textos e exemplos de apresentação desta aula foram preparados pela professora Andréia Zanchetti para o Blog do Enem. Andréia é formada em Matemática pelo IFRS e possui mestrado pela FURG.
