Sólidos geométricos: poliedros e corpos redondos
Entender os princípios da geometria espacial é fundamental para estudar os sólidos geométricos e suas características. Revise Matemática para o Enem!
Nesta aula de geometria espacial, vamos lembrar o conceito de cada um dos sólidos geométricos. É hora de revisar e aprender algumas propriedades muito importantes, que vire e mexe estão aparecendo nas questões matemática do Enem e dos vestibulares. Pronto para começar?
O que são sólidos geométricos
Na geometria espacial, os sólidos geométricos são os objetos que possuem comprimento, largura e altura, ou seja, são objetos tridimensionais. Eles são classificados em duas categorias, as quais são: poliedros e corpos redondos.
Classificando os sólidos geométricos: poliedros
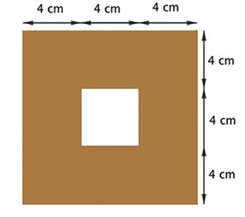
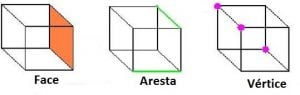
Os poliedros são figuras geométricas sólidas (não planas) formadas exclusivamente por figuras planas. São exemplos: o paralelepípedo, o cubo, o tetraedro e hexaedro. Podemos estudar também, os elementos dos poliedros. Você saber dizer um elemento do poliedro? São eles: aresta, vértice e face. Veja na imagem:
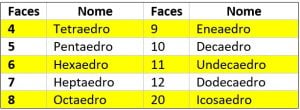
A nomenclatura dos poliedros é feita de acordo com a quantidade de faces. Veja a tabela que fizemos para você com a classificação dos principais poliedros:
As classes dos poliedros: prismas e pirâmides
Os poliedros ainda são separados em duas classes: prismas e pirâmides. A diferença entre eles é a quantidade de bases que eles possuem. Vamos contar essas bases então?
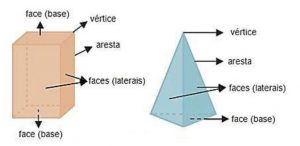
Prismas: são poliedros que possuem duas bases. Suas faces laterais são formadas por paralelogramos ou retângulos. Podemos ainda classificar os prismas em oblíquos e retos.
Pirâmide: são poliedros que possuem uma única base. Suas faces laterais são formadas por triângulos.
A fim de entender melhor a classificação dos prismas, acompanhe este vídeo do professor Sarkis:
Existem vários problemas que envolvem os poliedros e as pirâmides. Mas calma, não fique desesperado (a)! Temos um segredinho para você resolver esses probleminhas. Na verdade, é uma fórmula matemática. Ela é bem conhecida. Utilizamo-la na resolução da maioria dos problemas, principalmente, naqueles que caem em vestibulares, Enem e concursos. Já sabe de quem estou falando? É da relação de Euler.
Relação de Euler
A relação de Euler é uma equação que podemos determinar a quantidade de vértices, arestas e faces de um poliedro convexo e alguns não convexos. Veja:
V-A+F=2
V=número de vértices
A=número de arestas
F=número de faces
Veja o exercício a seguir, vamos resolvê-lo aplicando a relação.
Exemplo 01: (FAAP – SP) Em um poliedro convexo, o número de arestas excede o número de vértices em 6 unidades. Qual o número de faces?
Solução:
Seja V = quantidade de vértices do poliedro, como a quantidade de arestas excede o número de vértices em 6 unidades, a quantidade de arestas é expressa pela equação A = V + 6. Substituindo essas igualdades na relação de Euler obtemos:
V- (V + 6)+F= 2
Aplicando a distributiva temos a seguinte igualdade:
V – V- 6 + F= 2
F = 2+6
F = 8
Portanto, o poliedro possui 8 faces.
Exemplo 02: Um designer está projetando um objeto na forma de um poliedro convexo formado por 8 faces triangulares e 2 pentagonais. Determine o número de vértices desse poliedro.
Solução:
Primeiro devemos calcular a quantidade total de faces e arestas do poliedro, para depois aplicarmos a relação de Euler. Pensemos juntos!
Para a quantidade de faces devemos somar as faces triangulares com as faces pentagonais.
F = 8 + 2
F = 10
Para a quantidade de arestas, vamos pensar da seguinte maneira:
Se 1 face triangular possui 3 arestas, então 8 faces triangulares possuem 24 arestas, pois basta fazer 8 x 3 = 24. Mas, não podemos esquecer que estamos contando cada aresta duas vezes, por esse motivo dividiremos o total de arestas por 2, ou seja,
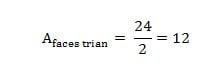
Faremos o mesmo para as faces pentagonais.
Se 1 face pentagonal possui 5 arestas, então 2 faces pentagonais possuem 10 arestas, pois basta fazer 5 x 2 = 10. Também devemos dividir esse número por 2, pois ocorre a mesma situação citada no cálculo das arestas das faces triangulares, ou seja,
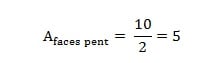
Logo, somando as arestas dos dois tipos de faces temos que o número de arestas é:
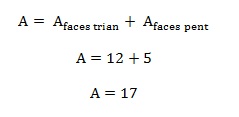
Agora que já temos a quantidade de faces e arestas, vamos substituir os valores encontrados na relação de Euler para determinar a quantidade de vértices.
V- A + F= 2
V – 17 + 10 = 2
V = 2-10+17
V = 9
Portanto, o poliedro possui 9 vértices.
Alguns poliedros possuem propriedades peculiares. Eles são chamados de Poliedros de Platão, e é o que abordaremos a seguir.
Poliedros de Platão
Os poliedros de Platão são poliedros regulares convexos que satisfazem três propriedades, as quais são:
- O número de arestas é igual em todas as faces;
- Os ângulos poliédricos possuem o mesmo número de arestas;
- Vale a relação de Euler;
Existem apenas 5 poliedros de Platão, anote aí o nome deles de acordo com a imagem a seguir.
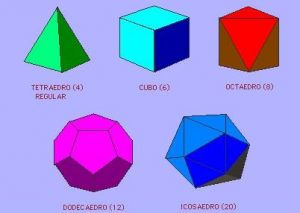
Vamos esquecer um pouquinho os poliedros e verificar a outra categoria dos sólidos geométricos, a dos corpos redondos.
Corpos redondos
Corpos redondos são figuras sólidas que não são formadas totalmente por figuras planas. São exemplos: esferas, cilindros e cones.
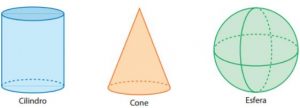
Sabe o que podemos fazer com esses sólidos? Podemos calcular o volume deles.
Para saber mais detalhes sobre os corpos redondos, confira a videoaula do nosso canal:
Volume dos sólidos geométricos
Calculamos o volume dos sólidos geométricos através do produto entre a área da base e a altura do sólido. Matematicamente falando, a fórmula do volume dos sólidos geométricos é:
V = Abase x h
Abase = área da base
h = altura do sólido
Vamos resolver mais um exercício.
Exemplo 03: (Enem – 2012) Alguns objetos, durante a sua fabricação, necessitam passar por um processo de resfriamento. Para que isso ocorra, uma fábrica utiliza um tanque de resfriamento, como mostra a figura.
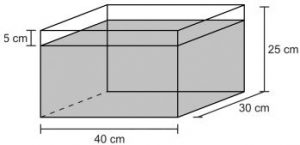
O que aconteceria com o nível da água se colocássemos no tanque um objeto cujo volume fosse de 2.400 cm3?
Solução:
Para saber o que aconteceria, devemos calcular o volume que a água ocupa e o volume do tanque apresentado na imagem acima, cuja forma é de um hexaedro. Começaremos calculando a área da base. A base do sólido é um retângulo de comprimento 40 cm e largura 30 cm.
Abase = 40cm x 30cm
Abase =120cm²
Agora, podemos calcular o volume do sólido cuja altura é 25cm.
V = Abase x h
V = 120cm² x 25cm
V = 3.000cm³
Logo, como a capacidade (volume) do tanque é de 3.000 cm³. O cálculo do volume do tanque é análogo ao volume do tanque, exceto a medida da altura. Pois a água não está até a borda do tanque, assim devemos descontar essa variação da altura, ou seja,
h2 = 25cm – 5cm
h2 = 20cm
Portanto, o volume da água será:
Vágua = 120cm² x 20cm
Vágua = 2.400cm³
Por fim, devemos somar o volume da água com o volume do objeto cujo volume é 2.400 cm³.
Vtotal = 2.400cm³ + 2.400cm³
Vtotal = 4.800cm³
Como o volume do tanque é 3.000 cm³ e o volume da água mais o objeto é maior que a capacidade do tanque, a água transbordaria.
Videoaula sobre poliedros
Para complementar seus estudos de geometria espacial, assista à videoaula a seguir. Nela, o professor Sarkis, de Matemática, explica tudo sobre poliedros.
Exercícios sobre sólidos geométricos
.