Inequações: o que são e como resolver
Você que está estudando para as provas do Enem e vestibulares, já está com todos os conteúdos em dia? Dá uma olhada na diversidade de inequações desse post e confere se não esqueceu de estudar nada!
Se você está em dia com os estudos em português, deve saber que o prefixo in- pode significar privação ou negação. Nesse caso, quando falamos de inequações estamos nos referindo à uma não–equação. Mas, o que isso significa? Parece não ter muito sentido ao ler dessa forma, mas se você for parar para analisar equações e inequações são bem parecidas.
A diferença é que a equação representa uma igualdade e a inequação representa uma desigualdade. Maiores, menores, maiores ou iguais, menores ou iguais, enfim, as inequações aumentam as possibilidades de resultado. Dessa maneira, aumentam também as possibilidades de resolução. Ficou curioso(a)? Então acompanha essa aula de Matemática para o Enem para aprender um pouco mais sobre as inequações!
Desigualdades
As inequações são expressões matemáticas que, diferentemente das equações (que utilizam somente a igualdade), utilizam na sua formatação os seguintes sinais de desigualdades:

Levando esses sinais de desigualdade em consideração, vamos ver alguns tipos de inequações e como resolvê-las. Mas, antes de tudo, é bom você relembrar como resolver uma inequação do primeiro grau, muito semelhante à equação de primeiro grau.
Inequação produto
Solucionar uma inequação produto é basicamente encontrar os valores de x que satisfaçam a inequação. Para isso utilizamos o estudo do sinal de uma função.
Vamos utilizar a multiplicação de duas inequações de primeiro grau como exemplo. Mas pode haver exercícios em que inequações de segundo grau precisem ser resolvidas. De qualquer forma, a maneira de resolver segue a mesma lógica.
Exemplo: Resolver a inequação produto ![]()
Vamos “desmembrar” essa inequação em duas equações e determinar a raiz de cada uma delas. Depois verificamos a posição da reta em relação ao eixo x. Veja:


Não esqueça! Faça o estudo do sinal prestando atenção no fato de que a inequação inicial requer os números maiores que zero .
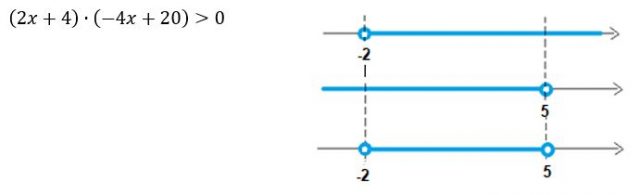
Assim, o conjunto solução da inequação é
![]()
Ou ainda, na representação por intervalo:
![]()
Como resolver inequação produto
Assista à videoaula do prof. Lucas ensinando a resolver inequação produto:
Inequação quociente
Para solucionar uma inequação quociente, as ferramentas matemáticas utilizadas são as mesmas do que na inequação produto, mas é preciso prestar atenção! Por se tratar de um quociente, é preciso lembrar que o denominador nunca pode ser igual a zero.
Exemplo: Encontre as soluções da seguinte inequação quociente:
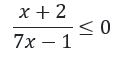
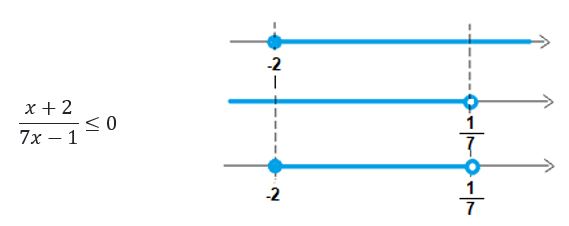
Passos: Primeiramente precisamos “desmembrar” essa inequação em duas equações e determinar a raiz de cada uma delas. Depois verificamos a posição da reta em relação ao eixo x. Veja:
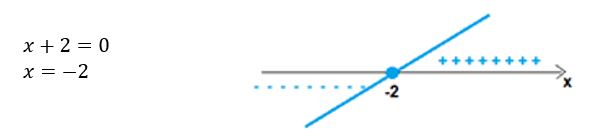
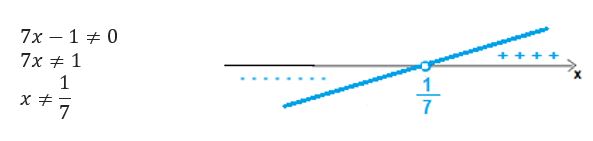
O intervalo é aberto pois o número ![]() zera o denominador.
zera o denominador.
Assim, o conjunto solução da inequação é
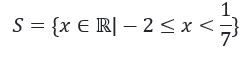
Ou ainda, na representação por intervalo:
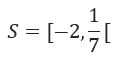
Como resolver inequações quociente
Assista também ao vídeo sobre inequações quociente:
Inequações do Segundo Grau
A solução das inequações de segundo grau se dá de forma bastante parecida com as inequações de primeiro grau. Para resolvê-las também fazemos o estudo do sinal a partir da raiz da equação. Para isso, basta somente lembrar que a equação de segundo grau admite até duas raízes.
Além disso, o gráfico se comporta de forma diferente: na função do primeiro grau o gráfico é uma reta, já na função do segundo grau é uma parábola, vamos ver como funciona?
Exemplo:
Encontre o conjunto solução da inequação: ![]()
Antes de tudo vamos reorganizar a inequação para que possamos calcular as raízes, temos então que
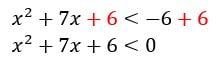
Calculando como equação para determinar as raízes
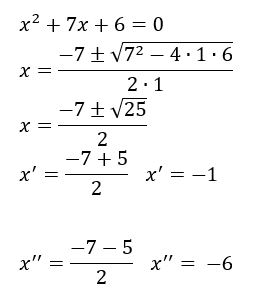
As raízes da equação ![]() são
são ![]() e
e ![]() . Por
. Por ![]() ser positivo
ser positivo![]() , o gráfico se comporta da seguinte forma:
, o gráfico se comporta da seguinte forma:
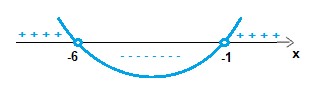
Logo, já que a inequação inicial requer os valores menores que zero, o conjunto solução é
![]()
Videoaula sobre inequações do 2º grau
A gente também preparou um vídeo sobre inequações do segundo grau, bora revisar?
Inequações exponenciais, logarítmicas e modulares
Para o estudo das inequações exponenciais, logarítmicas e modulares seguimos utilizando as mesmas ferramentas das inequações anteriores, resolvendo normalmente e prestando atenção nas condições de existência.
- Exponencial
Relembre as propriedades da equação exponencial e as utilize para resolver a inequação. Agora, veja o exemplo:
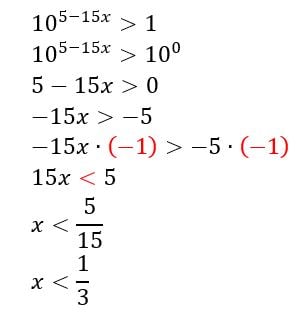
O conjunto solução da inequação é: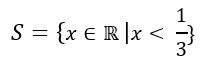
- Logarítmica
Reveja alguns conceitos e propriedades dos logaritmos. Agora, veja o exemplo:
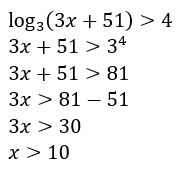
Além disso, 3x + 51 também tem que ser maior que zero, então:
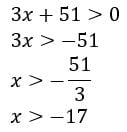
Fazendo o estudo do sinal: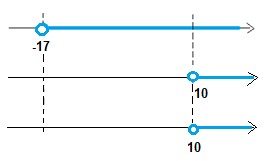 Logo o conjunto solução da inequação logarítmica é:
Logo o conjunto solução da inequação logarítmica é:
![]()
- Modular
Vamos resolver a seguinte inequação para entender esse tipo de resolução:
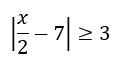
Para que o módulo tenha valor ![]() basta que:
basta que:
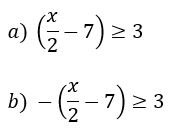 Então teremos:
Então teremos:
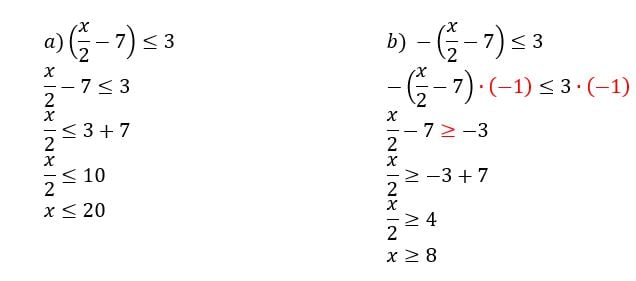
Fazendo o estudo do sinal:
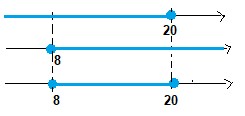
Então, o conjunto solução da inequação modular é:
![]()
Quer videoaula do prof. Lucas sobre inequações modulares também? É só dar o play! 😀
Exercícios
Questão 01)
Quantas soluções inteiras tem a inequação abaixo:
x² – 10x + 21 ≤ 0
a) 3
b) 4
c) 5
d) 6
e) 7
Questão 02)
Considere S o conjunto solução da inequação x6 – 25x² ≤ 0 e assinale a alternativa correta.
a) S ⊃ 0
b) S ⊂ R+
c) S ⊂ ]-3, 3[
d) S ∈ [-10, 10]
Questão 03)
O conjunto de todos os números reais x que satisfazem a inequação |x² – 2| < 1 é:
a) (-1, √3)
b) (-√3, √3)
c) (-1, 1)
d) (-√3, 0) ∪ (0, √3)
e) (-√3, -1) ∪ (1, √3)
Gabarito:
- C
- C
- E




