Grandezas diretamente ou inversamente proporcionais
Já parou pra pensar em quantas questões de equivalência entre grandezas costumam cair na prova do Enem? E não é só na prova de matemática não, até para a prova de química e de física você precisa estar preparado para o que der e vier. Vamos nessa?
As relações de dependência entre grandezas podem ser facilmente observadas no nosso dia a dia. Uma grandeza é tudo o que é suscetível de ser acrescentado ou diminuído.
Sendo assim, se uma grandeza pode ser acrescida ou diminuída e ao mesmo tempo se relacionar com outra grandeza, significa que dependendo da relação estabelecida entre as duas, essa segunda grandeza também vai ser acrescida ou diminuída de algum valor.
Relações entre grandezas
Nesta aula vamos aprender a identificar as diferenças entre grandezas diretamente proporcionais e grandezas inversamente proporcionais para que você chegue com tudo na hora da prova do Enem!
Comprimento, massa, velocidade, tempo, volume, capacidade e temperatura são alguns exemplos de grandezas que constantemente aparecem no nosso dia a dia.
Resumo sobre as Grandezas fundamentais
Confira agora com o professor Flaverson Messias, do canal do Curso Enem Gratuito,.uma introdução básica:
As grandezas podem se relacionar entre si, como por exemplo, ao calcularmos a velocidade, relacionamos o espaço percorrido com o tempo. Ou seja, uma medida de comprimento com uma medida de tempo.
As grandezas relacionadas podem ser classificadas de duas diferentes formas: grandezas diretamente proporcionais e inversamente proporcionais. A seguir, iremos detalhar cada uma delas.
Grandezas diretamente proporcionais
As grandezas diretamente proporcionais se relacionam entre si, assim como nome sugere. De uma forma bem direta, quando uma grandeza aumenta ou diminui, a outra aumenta ou diminui proporcionalmente. Mas o que isso significa? Observe o exemplo abaixo e entenda:
Exemplo 1: Quando uma pessoa fala que seu veículo faz 13 por 1, ela está querendo dizer que este veículo percorre 13 km com 1 litro de combustível. Em uma viagem de 1600 km, quantos litros de combustível serão gastos?
Resposta: Perceba que as grandezas que estão sendo relacionadas são diferentes entre si. Estamos relacionando uma medida de comprimento, que é o quilômetro, e uma medida de capacidade, que é o litro.
Geralmente, para solucionar questões como essa, utilizamos a famosa regra de três, montando o esquema
13 km equivale 1 L
1600 km equivale x L
Resultando em:
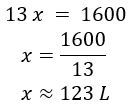
Ou seja, serão gastos aproximadamente 123 litros de combustível para fazer uma viagem de 1600 km.
Perceba como ao aumentarmos o percurso, a quantidade de combustível também aumentou. Esse aumento ocorreu de uma forma diretamente proporcional. A recíproca também é verdadeira: se diminuirmos o percurso, o consumo de combustível também é menor.
Grandezas inversamente proporcionais
Neste caso, podemos utilizar a mesma lógica do nome sugestivo para dizer que grandezas são inversamente proporcionais quando se relacionam entre si de forma inversa.
Ou seja, quando operações inversas são utilizadas nos cálculos. Sendo assim, se triplicarmos uma grandeza, a outra é dividida por 3; se elevarmos uma grandeza ao quadrado, na outra é aplicada a raiz quadrada.
A grosso modo, pode-se dizer que grandezas são inversamente proporcionais quando uma aumenta e a outra diminui, e vice-versa.
Um exemplo clássico de grandezas inversamente proporcionais são o tempo e a velocidade. Quando a velocidade aumenta, o tempo de deslocamento de um ponto até outro diminui.
Grandezas Escalares x Grandexas Vetoriais
Aprenda agora,de uma vez por todas, como diferenciar as Grandezas Escalares das Grandezas Vetoriais com o professor Flaverson Messias:
Veja como resolver exercício de grandezas
Exemplo 2: Qual é a velocidade de um trem que gasta 2 horas em um percurso, sabendo que gastaria 6 horas nesse mesmo percurso se estivesse a 30 km/h?
Resposta: Para solucionar esse exemplo você precisa lembrar das regrinhas utilizadas na regra de três.
Então, construímos uma proporção entre a velocidade do automóvel e o tempo gasto no percurso. essa proporção é:
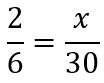
Por se tratar de grandezas inversamente proporcionais, utilizamos uma técnica de resolução onde inverte-se uma das razões da proporção apresentada acima. Depois, calcula-se normalmente a regra de 3.
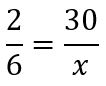
Aplicando a propriedade fundamental das proporções, teremos:
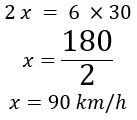
Ou seja, a velocidade do trem ao realizar o percurso em 2 horas é maior do que a velocidade em que ele estava ao realizar o percurso em 6 horas. No percurso de 2 horas a velocidade foi de 90 km/h e no percurso de 6 horas foi de 30 km/h.
As relações entre grandezas
E então? O que achou dessa aula? Para fixar bem o conhecimento sobre as relações entre grandezas, assista ao resumo em vídeo feito pelo professor Lucas Borguezan! A videoaula também está disponível no canal do Curso Enem Gratuito no YouTube.
Exercícios sobre Grandezas
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(FPS PE/2019)
A heparina é uma substância que atua como anticoagulante em várias patologias. Um médico receitou a um paciente 120 unidades de heparina por quilo de peso, a cada hora. A heparina disponível é uma solução na concentração de 1000 unidades de heparina para cada 50 mililitros. Se o paciente pesa 75 quilos, quantos mililitros da solução devem ser administrados ao paciente em cada minuto?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre grandezas e relações de dependência para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(UNCISAL/2019)
A régua, o barbante e o mapa mostrados a seguir foram utilizados por um estudante para fazer o seguinte procedimento a fim de calcular o comprimento do Rio Amazonas:
- cobriu com o barbante a linha do mapa que representa o Rio Amazonas, desde a nascente até a foz;
- esticou o barbante;
- mediu com a régua o comprimento do barbante e obteve 14,8 cm;
- verificou que o mapa foi construído na escala 17: 800 000 000.
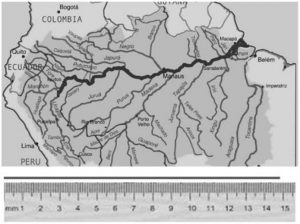
Disponível em: https://upload.wikimedia.org. Acesso em: 23 nov. 2018 (adaptado). Considerando-se a escala utilizada na construção do mapa e o comprimento do barbante, qual é o valor que mais se aproxima do comprimento do Rio Amazonas?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre grandezas e relações de dependência para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(UNCISAL/2019)
As equipes M e N classificaram-se para disputar o título anual de um campeonato de voleibol. A equipe campeã, aquela que conseguir 7 vitórias sobre a outra, ganhará R$ 360.000,00 como prêmio. Devido a problemas estruturais no ginásio em que as partidas aconteciam, a disputa foi encerrada quando a equipe M possuía 6 vitórias e a equipe N, 4 vitórias. Considerando esse placar, as equipes decidiram que a forma mais justa de dividir o prêmio, seria fazê-la de forma proporcional às probabilidades de uma ou outra ser campeã, se as partidas restantes viessem a ser disputadas no “cara ou coroa”.
Nas condições acordadas entre as equipes, as quantias que M e N, respectivamente, deverão receber são
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre grandezas e relações de dependência para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(PUCCampinas SP/2019)
Um motorista pretendia percorrer a distância entre duas cidades desenvolvendo a velocidade média de 90 km/h (1,5 km/min). Entretanto, um trecho de 3,0 km da estrada estava em obras, com o trânsito fluindo em um único sentido de cada vez e com velocidade reduzida. Por esse motivo, ele ficou parado durante 5,0 minutos e depois percorreu o trecho em obras com velocidade de 30 km/h (0,5 km/min). Considerando que antes de ficar parado e depois de percorrer o trecho em obras ele desenvolveu a velocidade média pretendida, o tempo de atraso na viagem foi
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre grandezas e relações de dependência para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(FATEC SP/2019)
Um grupo de alunos do curso de Jogos Digitais da FATEC inicia a produção de um jogo. Após 6 horas de trabalho, verificam que conseguiram finalizar apenas 24% do jogo. Para poder concluir o restante dele, esse grupo de estudantes pede ajuda a alguns amigos, conseguindo duplicar o tamanho da equipe.
Assinale a alternativa que apresenta o tempo total de produção do jogo.
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre grandezas e relações de dependência para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(IFBA/2019)
Um grupo de 80 motoqueiros viaja por 60 dias e suas motos totalizaram um consumo de 10000 l. Se este mesmo grupo tivesse sido composto com 20 motoqueiros a menos, em quantos dias neste grupo, suas motos totalizariam um consumo de 8000 l, supondo todas as motos com mesmo rendimento de consumo?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre grandezas e relações de dependência para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(IFSC/2019)
Em uma lanchonete, atualmente, 2 trabalhadores preparam 10 sanduíches em 5 minutos. Os responsáveis pela empresa perceberam que em certos horários é necessário preparar 12 sanduíches em 3 minutos. Considerando que os responsáveis busquem contratar trabalhadores que exerçam o trabalho no mesmo ritmo que os demais, para suprir a demanda nesses horários, é necessário contratar mais:
Assinale a alternativa CORRETA.
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre grandezas e relações de dependência para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(IFSC/2019)
Quatro pedreiros, trabalhando 8 horas por dia, constroem 15m de muro em 5 dias. Sabendo-se que todos os pedreiros trabalham no mesmo ritmo e que dois pedreiros adoeceram e se ausentaram do trabalho, quantos dias serão necessários para construir 18m de muro, trabalhando-se 6 horas por dia:
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre grandezas e relações de dependência para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(UNIFOR CE/2019)
A escassez de água é um problema ambiental cujos impactos tendem a ser cada vez mais graves. Em virtude da seca, um município cearense passava por situação de racionamento de água, fazendo com que os moradores recebessem o fluxo de água em dias alternados. Por conta disso, um morador desse município resolveu encher de água um tanque com três torneiras I, II e III. A torneira I enche o tanque em nove horas, enquanto a torneira II enche o tanque em dose horas. Se as torneiras I e II funcionarem juntas e, com elas, a torneira III, o tanque ficará cheio em quatro horas. Considerando que a vazão das torneiras I, II e III é sempre constante, em quantas horas a torneira III enche o tanque?
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre grandezas e relações de dependência para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(FUVEST SP/2018)
Dois atletas correm com velocidades constantes em uma pista retilínea, partindo simultaneamente de extremos opostos, A e B. Um dos corredores parte de A, chega a B e volta para A. O outro corredor parte de B, chega a A e volta para B. Os corredores cruzam)se duas vezes, a primeira vez a 800 metros de A e a segunda vez a 500 metros de B. O comprimento da pista, em metros, é
CorretoParabéns! Siga para a próxima questão.
IncorretoResposta incorreta. Revise o conteúdo nesta aula sobre grandezas e relações de dependência para acertar na hora da prova!

Sobre o(a) autor(a):
Andréia Zanchetti - Os textos e exemplos de apresentação desta aula foram preparados pela professora Andréia Zanchetti para o Blog do Enem. Andréia é formada em Matemática pelo IFRS e possui mestrado pela FURG.
Gostou? Compartilhe!
Continue lendo:
Aqui vão 2 publicações relacionadas que talvez você goste:

Como resolver a prova de Matemática no Enem 2024? Veja as dicas do professor
Por Melina Zanotto | 08 de novembro
Confira as orientações e estratégias do professor Lucas Borguezan para se sair bem na prova de Matemática no Enem 2024.

Aulão Enem de Matemática: revisão intensiva e gratuita para a prova
Por João Vianney dos Valles Santos | 11 de outubro
Assista ao Aulão Enem de Matemática do Curso Enem Gratuito e revise os conteúdos mais importantes para a prova.


